Министерство образования и науки Российской Федерации
Нижегородский государственный университет им. Н.И. Лобачевского
Национальный исследовательский университет

Кафедра общей физики

Семиков С.А.

    В пособии рассмотрены основные методы компрессии лазерных импульсов, включая метод компрессии чирпированных импульсов и перспективные методы компрессии. Также рассмотрены главные применения компрессированных ультракоротких импульсов.

    Методическая разработка предназначена для студентов, магистрантов и аспирантов ННГУ, специализирующихся в области лазерной физики (направления: 010400 "Информационные технологии", 010800 "Радиофизика"; специальности 010802 "Фундаментальная радиофизика и физическая электроника", 230201 "Информационные системы и технологии").

© Нижегородский государственный
университет им. Н.И. Лобачевского, 2011

– Ладно. Становись в очередь. Но только для компрессии!
Кузнец Филимон из фильма "Не валяй дурака"

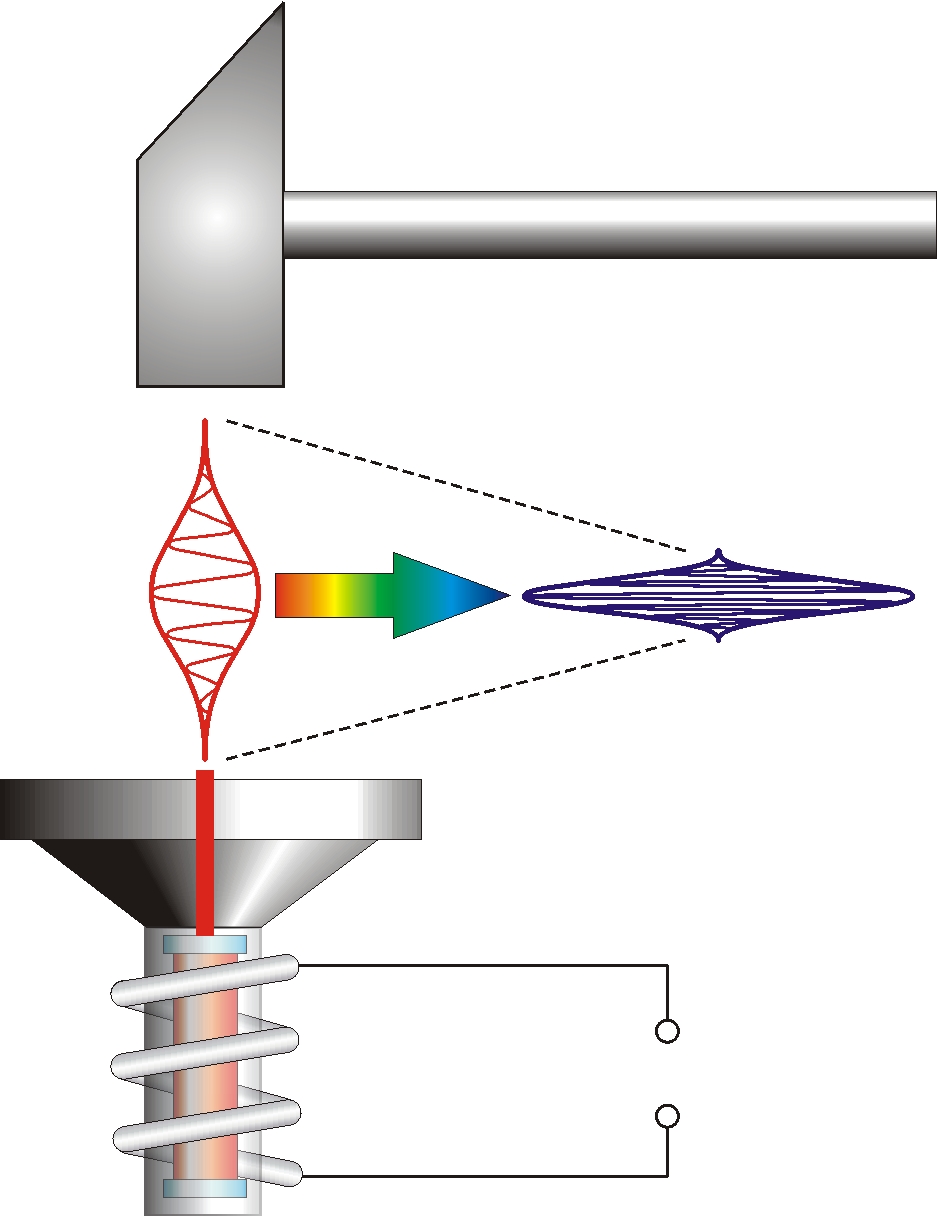
    Методы компрессии лазерных импульсов широко применяют для получения ультракоротких импульсов субпикосекундной и фемтосекундной длительности. Эти методы позволяют сжать исходный импульс лазерного генератора, имеющий длительность в нано- и пикосекунды (10^–9–10^–12 с), в сотни и тысячи раз (до 10^–13–10^–15 с). При таких длительностях протяжённость импульса в пространстве составляет микроны. Кроме того, путём сжатия лазерного импульса (слово "компрессия"– от фр. compression – сжатие) сильно повышают его мощность, раз по закону сохранения вся энергия импульса, распределённая в сравнительно широком временном интервале, концентрируется после сжатия в предельно коротком интервале времени (рис. 1). Такая временнáя фокусировка энергии приводит к существенному повышению мощности, интенсивности излучения вплоть до петаватных мощностей (10¹⁵ Вт), подобно тому как пространственная фокусировка с помощью линз (или зеркал) существенно повышает яркость излучения, собирая весь свет, прошедший широкую апертуру линзы (или параболического зеркала), в маленьком фокальном пятне. Таким образом, современные методы компрессии уже во временнóй области реализуют древнюю технологию Архимеда, который сжёг неприятельский флот солнечным светом, сфокусированным упорядоченно выстроенными и координировано управляемыми зеркальными щитами – прообразом современных фазовых антенных решёток. А нижегородец И.П. Кулибин (инженер, оптик и вероятный прообраз лесковского Левши) собрал из зеркал первый в мире прожектор (прообраз "гиперболоида инженера Гарина" и лазера) – рукотворное солнце, излучающее мощный параллельный пучок света. Так и современные Архимеды и Кулибины, работая с "рукотворным солнцем" – мощным лазерным излучением, широко применяют для компрессии зеркала, отражательные дифракционные решётки, а также особые брэгговские зеркала и световоды, о чём далее и расскажем.

    В целом осуществляемая оптиком компрессия импульсов, ведущая к их обострению и повышению мощности в ходе сжатия, напоминает обработку кузнецом заготовок, которые под ударами молота становятся не только много тоньше, но и в силу сохранения объёма металла – заметно выше, острее, превращаясь из безликого слитка металла в эффективное орудие труда. Вот и лазерный импульс-заготовка превращается компрессионным устройством в острое, мощное и эффективное орудие с набором полезнейших свойств и применений, включая прецизионную обработки материалов и ряд других практических и научных приложений. О методах компрессии и расскажем по очереди.

    Столь мощное и короткоимпульсное излучение используют для многих целей, в том числе для прецизионной обработки материалов, оптической записи и передачи информации, для хирургических операций, а главное,– для создания многочисленных нелинейных эффектов, позволяющих получить излучение с новыми свойствами, спектральными характеристиками и применениями. Основное свойство ультракоротких лазерных импульсов – высокая пиковая мощность при малой длительности и умеренной средней мощности, позволяет воздействовать на материалы локально в пространстве и во времени, не затрагивая прилегающие слои вещества, что неизбежно происходило при обработке непрерывным лазерным излучением или лазерными импульсами обычной длительности, что вызывало сильный нагрев и повреждение материалов. А предельно короткий лазерный импульс позволяет производить плавление и испарение (абляцию) материала в пределах строго ограниченной области, не вызывая нагрева и изменения структуры материала в прилегающих участках. Это позволяет производить прецизионную обработку материалов, например, прорезать тончайшие отверстия не только в металлических деталях, но и в стекле, кристаллах, которые из-за своей хрупкости очень чувствительны к резкому перепаду температур из-за неравномерного теплового расширения, которое ведёт к образованию трещин и разрушению кристаллов. Поэтому именно обработка ультракороткими лазерными импульсами, которые мгновенно испаряют облучаемый материал, без нагрева прилегающих участков, позволяют пробивать отверстия в алмазных фильерах (применяемых для вытягивания вольфрамовых нитей) и рубиновых подшипниках – часовых камнях [1]. Кроме того, такая мягкая и быстрая абляция необходима в хирургических операциях (особенно на глазах), поскольку повышение температуры тканей всего на несколько градусов ведёт к отмиранию клеток, а дальнейшее повышение температуры вызывает свёртывание белков – необратимое изменению их структуры и свойств.

    Повышение пиковой мощности (то есть мгновенной мощности в максимуме, на пике импульса) достигается, как говорилось, за счёт того, что вся энергия импульса W, исходно распределённая в протяжённом интервале времени Δt собирается после компрессии в предельно малом временном интервале Δt' (Рис. 1). В итоге, если энергия в ходе компрессии почти не теряется W≈PΔt≈P'Δt', то исходная мощность излучения P≈W/Δt увеличится до значения P'≈W/Δt',– в той же мере, в какой сократится импульс P'=PΔt/Δt'. Пропорционально вырастет также интенсивность излучения I'=IΔt/Δt', то есть мощность, поступающая в единицу площади (I=dP/dS). Иначе говоря, в силу сохранения энергии при компрессии сохраняется площадь под графиком интенсивности или мощности импульса, которая равна энергии импульса. Именно поэтому такая трансформация импульса напоминает деформацию под ударами молота металлической заготовки, которая, уплощаясь, почти не меняет площади поперечного сечения, отчего по мере сжатия становится в другом направлении всё шире и острее. Эти заготовки-импульсы по очереди подходят к компрессирующему устройству и преобразуются в автоматную очередь из ультракоротких импульсов – "световых пуль" [2].

    Особенно важна предельно малая длительность импульсов для создания нелинейных эффектов. С одной стороны, компрессия импульсов позволяет достигнуть тех высоких критических интенсивностей излучения, которые необходимы для проявления нелинейных эффектов. С другой стороны, за счёт малой длительности импульса его энергия оказывается невелика, достигая наноджоулей. Соответственно, и средняя мощность оказывается невелика и недостаточна для разрушения материала нелинейной среды. Если ту же мощность подавать в виде более длинных импульсов, а тем более – в виде непрерывного излучения, то средняя мощность окажется столь велика, что разрушит материал. То есть условие появления нелинейных эффектов (критическая интенсивность) оказывается несовместимым с условием сохранения свойств нелинейной среды (с его оптической прочностью – средней интенсивностью излучения, разрушающей нелинейный материал). Таким образом, ряд нелинейных эффектов можно наблюдать лишь под действием ультракоротких импульсов излучения. Среди таких эффектов: вынужденное комбинационное рассеяние света (когерентный эффект Рамана), фазовая самомодуляция, самофокусировка, 4-хволновое смешение и т.д. А при низкой оптической прочности нелинейного материала или при слабой нелинейности такие эффекты, как генерация высших гармоник, могут наблюдаться только под воздействием ультракоротких импульсов.

    Наконец, крайне малая длительность импульсов позволяет исследовать быстротекущие процессы, где необходимо высокое временное разрешение, в том числе для целей сверхбыстрой спектроскопии и КАРС-спектроскопии (скажем для анализа быстро меняющегося распределения и химического состава газов в камерах сгорания), для исследования быстро релаксирующих процессов (в том числе химических, ионизационных). Малая длительность импульса позволяет вдобавок выделять его из шума посредством синхронного детектирования: работа детектора синхронизована с работой импульсного генератора, за счёт чего он регистрирует сигнал только в предполагаемые моменты поступления импульсов. Благодаря этому, даже если средняя мощность импульса мала по сравнению со средней мощностью шумов (низкое отношение сигнал/шум), особенно при ослаблении сканирующего сигнала, его удаётся легко выявить путём синхронного детектирования, поскольку в пределах времени детектирования пиковая мощность сигнала оказывается заметно выше уровня шумов (особенно важна такая техника синхронного детектирования при спектроскопии и для регистрации терагерцовых импульсов, маскируемых тепловыми шумами). Важны ультракороткие и предельно короткие (с длительностью порядка периода светового поля) импульсы и для сверхбыстрой передачи информации посредством Волоконно-Оптических Линий Связи (ВОЛС). Ведь количество информации, передаваемой в секунду по одной линии (по одному оптическому каналу-волокну) пропорционально частоте следования импульсов (количеству импульсов в секунду), которая может быть сделана тем выше, чем короче импульс. Так, благодаря применению ультракоротких субпикосекундных лазерных импульсов, с периодом следования порядка 10^–12 с, удаётся осуществлять передачу информации по одному каналу со скоростью 1 Терабит в секунду (10¹² бит/с).

    Таким образом, компрессия лазерных импульсов играет важную роль для научных исследований и технических приложений. Далее рассмотрим конкретные способы, которыми осуществляют сжатие импульсов. Все эти способы, так же как ряд других современных электронных и лазерных технологий, были подсказаны радиотехникой, радиофизикой и радиоспектроскопией, где уже давно существовали отработанные технологии сжатия электрических и радиоимпульсов, скажем в приёмных трактах радиолокаторов [2]. Суть всех этих методов сводится к тому, что исходный импульс пропускают через линию задержки, которая неодинаково задерживает переднюю и заднюю часть импульса: передний фронт импульса задерживается сильнее, чем задний. В итоге, по мере движения вдоль линии задержки, хвостовая часть импульса всё больше догоняет головную, сокращая разрыв, а значит и длительность импульса, убывающую пропорционально пройденному пути. Общая идея оптической компрессии та же, зато сама реализация оптической линии задержки и способа, которым устанавливается неравная задержка для передней и задней части импульса, может сильно разниться в зависимости от методов компрессии, некоторые из которых рассмотрим ниже.

    Исторически первым где-то в 1980-х гг. возник метод компрессии, использующий в качестве линий задержки среды с дисперсией. Ведь диспергирующая среда как раз оказывает на свет разных длин волн различное замедляющее действие: показатели преломления, характеризующие степень этого замедления и снижение скорости света, различаются для излучения разных частот, разных цветов. Благодаря этому стеклянная призма, в качестве дисперсионного элемента, и разлагает белый свет в радужную полоску. Значит, если искусственно создать импульс, вдоль которого частота будет линейно меняться (скажем, передний фронт будет "окрашен" в синий цвет, а задний – в красный), то при прохождении через линию задержку с дисперсией оптический импульс станет сжиматься, поскольку головная "синяя" часть импульса в среде с нормальной дисперсией движется с меньшей групповой скоростью, чем хвостовая "красная", которая по мере движения всё больше догоняет переднюю, что и ведёт к сокращению импульса. Или, напротив, частоту несущей в импульсе можно линейно повышать (головная часть импульса содержит низкие частоты, а хвостовая – высокие). Тогда при пропускании импульса через линию задержки с аномальной дисперсией, где синие волны движутся быстрее красных, хвостовая высокочастотная часть импульса будет догонять переднюю высокочастотную, вызывая сокращение импульса. Такие частотно-модулированные сигналы, вдоль которых частота линейно меняется, называют чирпированными, от английского слова chirp – "чирик", "чириканье", поскольку звук, в котором тон постепенно повышается, напоминает чириканье воробья [2]. Именно такой звук повышающегося тона слышим при наполнении водой канистр и бочек, в которых по мере наполнения сокращается объём свободной резонансной полости, а значит сокращается и длина звуковой волны – понижается основная частота, излучаемая таким резонатором. Таким образом, первый метод компрессии сводится к созданию чирпированных импульсов и пропусканию их через линию задержки с дисперсией (Рис. 2).

    Фактически, этот метод пришёл из радиолокации, где тоже возникла задача компрессии импульсов для повышения их мощности, сильно спадающей после отражения радиосигнала от цели и прохождения больших дистанций. Поэтому радиолокационная станция излучает протяжённый чирпированный импульс, который после отражения от цели проходил в приёмном тракте линию задержки с дисперсией, отчего сжимался и за счёт происходящего при этом повышения мощности мог быть легко зарегистрирован (это так называемые чирп-радары, производимые, например, НИТЕЛ [2]). Принципиально компрессия оптических импульсов ничем не отличается от рассмотренной выше компрессии радиоимпульсов: разница лишь в частоте электромагнитного излучения. Поэтому существенно разнятся и методы, элементы, осуществляющие чирпирование и дисперсию.

    Как же осуществить чирпирование оптического импульса на практике? Казалось бы, самое простое решение – это пропустить исходный импульс через диспергирующую среду. Так, образующие импульс частотные составляющие, двигаясь в среде с нормальной дисперсией с разной скоростью, приведут к хроматической аберрации импульса во временной области: красные лучи, движущиеся с повышенной скоростью, окрасят переднюю часть импульса в красный цвет, а более медленные и отстающие синие лучи окрасят заднюю часть импульса в синий цвет. Дисперсия разлагает импульс на цвета во времени, также как призма за счёт дисперсии разлагает белую полоску на цвета, окрашивая один её конец в красный цвет, а другой – в синий. Поскольку ширина спектра импульса невелика и групповые скорости в пределах такого интервала частот меняются приблизительно линейно, то импульс по мере движения в среде будет равномерно расплываться, а частота будет линейно меняться вдоль импульса, то есть импульс станет чирпированным. Однако такое чирпирование не помогает, а только мешает, поскольку в дисперсионной среде импульс не только чирпируется, но и растягивается от неравенства групповых скоростей.

    Конечно, пропустив такой импульс через линию задержки в виде среды с аномальной дисперсией (где групповая скорость синих лучей уже будет превышать скорость красных), можно снова сжать импульс. Однако в ходе этого удастся разве что сжать импульс до исходной длительности, а сделать короче его не удастся. Тем не менее, такие устройства, снова сжимающие импульс после его неизбежного растяжения при прохождении диспергирующих элементов (линз, пластинок, кристаллов), широко применяют для компенсации этого нежелательного растяжения и называются компенсаторами дисперсии. Кроме того, такие, на первый взгляд, бесполезные циклы растяжения-сжатия импульса используют для его усиления. Поскольку усиление исходного импульса до рекордной мощности обычно приводит к пробою активной среды, то импульс сначала растягивают по указанной технологии диспергирующим элементом, названным эспандером (от англ. to expand – расширять, вытягивать). При этом интенсивность по закону сохранения энергии снижается (подобно утоньшению вольфрамовой нити при её вытягивании через алмазную фильеру). Затем этот растянутый импульс усиливают в активной среде – в усилителе, после чего импульс снова сжимают уже вне активной среды с помощью элемента с обратным знаком дисперсии – компрессора (от фр. compression – сжатие). Ещё раз отметим, что такой компрессор не сжимает импульс до длительности меньше исходной, а лишь восстанавливает его исходную длительность.

    Для сжатия импульсов до длительности меньше исходной применяют метод чирпирования на основе эффекта самомодуляции фазы (сокращённо – СМФ или ФСМ). Этот нелинейный эффект основан на том, что в сильных оптических полях показатель преломления среды n начинает зависеть от амплитуды электрического поля Е₀ и пропорциональной ей интенсивности излучения I~Е₀² по закону n=n₀+n₂Е₀², где n₀ – номинальный показатель преломления среды в области линейной оптики, а n₂ – коэффициент, характеризующий изменение показателя за счёт нелинейных свойств среды. Огибающая импульса обычно имеет колоколообразный гауссов профиль с высокочастотным заполнением – быстроменяющимся электрическим полем E, колеблющимся на частоте ν₀ лазерного излучения (рис. 3). При прохождении нелинейной среды световые волны на вершине импульса, где интенсивность I излучения максимальна, движутся с пониженной фазовой скоростью c/n, поскольку для такой интенсивности показатель преломления n=n₀+n₂Е₀² максимален, тогда световые волны у подножия импульса движутся в среде с фазовой скоростью близкой к номинальной c/n₀, поскольку на краях импульса интенсивность излучения нулевая. Из-за того, что на вершине импульса гребни волн отстают и отползают к заднему фронту, в хвостовой части импульса гребни световых волн уплотняются (длина волны сокращается), скапливаются (частота света повышается), а в головной части импульса, они напротив расходятся, разрежаются (длина волны растёт и частота понижается). В итоге импульс напоминает кузнечные меха или меха гармони, где нередко складки, гребни скапливаются с одной стороны, а с другой – расходятся.

    Таким образом, после прохождения импульсом нелинейной среды с показателем преломления n=n₀+n₂Е₀² набег фазы оказывается неодинаковым вдоль импульса – импульс получается фазомодулированным, причём сам же и производит модуляцию фазы своей переменной интенсивностью I (поэтому эффект и был назван фазовой самомодуляцией, или ФСМ). С другой стороны, каждый фазомодулированный сигнал можно рассматривать как частотно-модулированный. И действительно, как видели, сигнал оказывается частотно-модулированным, чирпированным: его головная часть содержит более длинные волны ("окрашена в красный цвет"), а хвостовая содержит более короткие волны ("окрашена в синий"), и в окрестностях вершины импульса частота меняется вдоль импульса почти линейно. Причём, что очень существенно для компрессии, при чирпировании импульса его длительность не изменилась.

    Пропустив такой чирпированный импульс через дисперсионную среду, его длительность можно существенно сократить, то есть осуществить компрессию. Легко видеть, что дисперсия такой линии задержки должна быть для этого аномальной: длинные волны должны двигаться медленней коротких, в отличие от сред с нормальной дисперсией, где красные лучи опережают синие. Дисперсию характеризуют через дисперсионный параметр D=dβ₁/dλ, где β₁=1/V_g – величина обратная групповой скорости V_g [3]. Дисперсионный параметр часто меряют в пикосекундах на нанометр, на километр: пс/(нм·км). Этот параметр, имеющий размерность времени, показывает, на сколько пикосекунд волны с длиной волны λ опередят за счёт разницы групповых скоростей V_g более длинные, с длиной волны λ+Δλ, большей на Δλ=1 нм, после прохождения пути в 1 км. Соответственно, нормальной дисперсии (длинные волны опережают короткие) отвечает D<0, тогда как аномальную дисперсию (короткие волны опережают длинные) характеризует D>0.

    Дисперсию можно выразить из дисперсионного уравнения k(ω), разлагая постоянную распространения (волновое число k) в ряд Тейлора по круговой частоте ω=2πν в окрестности частоты ω₀:

k(ω)=n(ω)ω/c=k(ω₀)+β₁·(ω-ω₀)+½β₂·(ω-ω₀)²+… .                (1)

Здесь β₁=[dk/dω]_ω=ω0=1/V_g(ω₀) и β₂=[d²k/dω²]_ω=ω0 – коэффициенты разложения. Коэффициент β₂ как раз и ответственен за дисперсию групповых скоростей и уширение импульса. Действительно, по определению групповая скорость

V_g(ω)=dω/dk=1/(dk/dω)≈1/[β₁+β₂·(ω-ω₀)]≈1/β₁–β₂·(ω-ω₀)/β₁²=V_g(ω₀)–β₂·(ω-ω₀)V_g²(ω₀).    (2)

    То есть, именно коэффициент β₂ характеризует зависимость групповой скорости от частоты ω, потому его и называют коэффициентом дисперсии. Коэффициент β₂ следующим образом связан с дисперсионным параметром D: β₂=-λ²D/2πc [3]. То есть нормальной дисперсии (D<0) соответствует β₂>0 (поэтому такую дисперсию называют ещё положительной), тогда как аномальной дисперсии (D>0) отвечает β₂<0 (отрицательная дисперсия).

    Само слово "аномальная" подразумевает, что среды с такой дисперсией – это нонсенс, поскольку обычным материальным средам свойственна нормальная дисперсия. Аномальная дисперсия есть разве что вблизи резонансных частот, на которых среда поглощает излучение (что нежелательно при работе с мощными лазерных импульсов), а также в плазменных средах, например в металле (где тоже велико затухание), в ионосфере для радиоволн. Но радиотехники и оптики легко нашли выход и давно создали искусственные элементы, для которых дисперсия остаётся аномальной в широком диапазоне частот, без поглощения и других нежелательных эффектов, о чём будет рассказано в разделе 4.1.

    Теперь рассмотрим, до каких пределов можно сжать импульс, применяя метод компрессии чирпированных импульсов. Известно, что для лазерного излучения характерна очень узкая спектральная линия, что имеет ряд важных применений. Однако для генерации коротких импульсов малая ширина спектральной линии Δν – это существенное ограничение, поскольку из соотношений спектрального анализа сигналов следует, что длительность импульса Δt не может быть меньше обратной ширины спектральной линии 1/Δν (точнее 1/2πΔν). И наоборот, ширина спектра Δν не может быть меньше обратной длительности импульса 1/Δt (точнее 1/2πΔt). Если записать это в виде ΔtΔν≥1/2π и помножить на постоянную Планка h, то получим чисто классическую интерпретацию принципа неопределённости Гейзенберга ΔtΔE≥h/2π, где ΔE=hΔν – неопределённость энергии фотонов. В связи с этим можно вспомнить мнимое подтверждение квантовомеханического принципа неопределённости Э. Лоуренсом – создателем первого циклотрона. Освещая атомы газа короткими импульсами света, он наблюдал уширение линий поглощения по мере сокращения длительности импульса, что якобы доказывало принцип неопределённости. А на деле наблюдался чисто классический эффект уширения спектра коротких импульсов, вытекающий из формул спектрального анализа сигналов, и всегда имеющий место, независимо от того, справедлива квантовая механика или нет. Так же и ряд других подтверждений принципа неопределённости основан на чистом недоразумении.

    Итак, для монохроматического света лазера узость спектральных линий Δν означает сравнительно большую длительность импульсов Δt – порядка 1/Δν. Сокращение длительности невозможно без параллельного уширения спектра Δν. Так, гелий-неоновый лазер, генерирующий непрерывное монохроматическое излучение, имеет очень узкие спектральные линии. А лазер, работающий в режиме модуляции добротности даёт уже короткие импульсы с длительностью порядка наносекунды. При этом спектр излучения уже существенно уширен. А, скажем, титан-сапфировый лазер, работающий в режиме синхронизации мод сразу выдаёт без чирпирования-компрессии готовые ультракороткие импульсы (порядка сотен фемтосекунд) за счёт того, что ионы титана в сапфире благодаря развитой системе уровней и их сдвигу по эффекту Штарка создают достаточно широкую частотную полосу усиления, допускающую генерацию ультракоротких импульсов. Впрочем, широкий спектр – это условие необходимое, но недостаточное для генерации коротких импульсов. Предельно малая длительность импульса 1/Δν (такой импульс называется спектрально-ограниченным или Фурье-ограниченным) достигается тогда, когда образующие его частотные составляющие имеют соответствующие фазы, связанные определёнными фазовыми соотношениями. В лазере с синхронизацией мод этой цели служит элемент, синхронно выпускающий частотные составляющие излучения, то есть синхронизирующий моды.

    По тому же принципу работает, по сути, и метод компрессии, который до сих пор описывали на пространственно-временном языке, а теперь рассмотрим на эквивалентном фазо-частотном языке. На первом этапе, при чирпировании импульса в нелинейной среде происходит уширение спектра: узкая спектральная линия превращается в сравнительно широкую полосу Δν (Рис. 3). Уширение может быть столь велико, что монохроматический свет лазера преобразуется в белый свет, содержащий все цвета радуги, то есть охватывающий весь или почти весь диапазон видимого света – такое излучение со сверхшироким белошумовым спектром называют суперконтинуумом (в дословном переводе с англ. "сверхпротяжённым"). Однако, несмотря на уширение спектра, полученный чирпированный импульс, как видели, не уменьшал, а сохранял свою длительность, то есть ещё не стал оптимизированным, спектрально ограниченным. Чтобы исправить эту недоработку, необходимо, как сказано, внести соответствующие фазовые поправки для каждой частотной составляющей. Именно это и делает дисперсионный элемент, который придаёт каждой спектральной составляющей импульса соответствующий фазовый сдвиг, благодаря чему импульс сокращается и, становясь спектрально ограниченным, приобретает минимально допустимую длительность порядка 1/Δν.

    Таким образом, именно ширина спектра Δν определяет минимальную длительность импульса, которой можно достичь, используя метод компрессии. Поскольку Δν≤ν=1/T, где ν – максимальная частота в спектре, а T – период светового поля, составляющий для видимого света несколько фемтосекунд (10^–15 с), то ясно, что импульс не может быть короче этого фундаментального предела в несколько фемтосекунд. Так, ещё в 1987 г. было осуществлено сжатие частотно модулированного импульса в диспергирующей среде до 6 фемтосекунд (около трёх периодов светового поля). А вскоре после этого тем же методом был получен импульс ИК-диапазона длиной в один период светового поля [4]. Более короткие импульсы таким способом получить нельзя. Единственный способ дальнейшего сокращения импульсов состоит в увеличении верхней частоты ν, то есть – в переходе из оптики в ультрафиолетовый и рентгеновский диапазон. Именно так получают импульсы аттосекундной длительности, о чём подробней расскажем далее.

    Итак, для рекордной компрессии импульсов необходимо обеспечить точные фазовые соотношения между частотными составляющими, или модами импульса. Это означает, что необходимо подобрать соответствующую длину дисперсионного элемента, которая в точности компенсировала бы набег фаз, возникший в ходе нелинейного преобразования импульса. Действительно, раз по мере движения импульса в среде с аномальной дисперсией и увеличения пройденного им пути z, "синяя" хвостовая часть импульса постепенно догоняет головную "красную", то на некотором расстоянии z_min они совпадут (частотная модуляция исчезнет). При этом импульс сожмётся до предельной длительности Δt_min=1/Δν, став спектрально ограниченным. Но при дальнейшем движении импульс снова начнёт растягиваться, поскольку высокочастотная часть импульса уже обгонит низкочастотную и, став головной, будет всё дальше уходить вперёд, растягивая импульс. Это постепенное сжатие, а затем растяжение импульса после достижения им предельно малой длительности на оптимальном расстоянии z_min отражено на графике (Рис. 4). Таким образом, расчёт компрессионной установки сводится к выбору нелинейной среды и дисперсионного элемента, в котором подбирается длина пути луча z_min из условия предельного сжатия импульса.

    Такое сжатие импульса во времени до предельно малой длительности (по мере движения в среде с дисперсией), а затем его расплывание, во многом напоминает сжатие собирающей линзой светового пучка, имевшего большой радиус, до предельно малого фокального пятнышка, а вслед за этим – снова расширение пучка в пространстве. Это показывает аналогию между дисперсионным расплыванием волновых пакетов и дифракционным расплыванием волновых пучков. При этом, если минимальная длительность импульса ограничена спектральным пределом – шириной частотного спектра импульса (спектрально ограниченный импульс), то размер фокального пятна (радиус перетяжки пучка) ограничен дифракционным пределом (шириной углового спектра). Чем шире частотный спектр и чем меньше период колебаний T, тем короче может быть импульс во времени. А чем шире угол, под которым собираются лучи в фокусе и чем меньше длина волны λ, тем меньше может быть фокальное пятно. За счёт такой временнóй и пространственной компрессии-фокусировки и растёт пропорционально интенсивность излучения. При временнóй компрессии это происходит за счёт сборки во временнóй области частотных компонент импульса. А при пространственной фокусировке – за счёт сборки в пространственной области пространственных компонент пучка (лучей). Чтобы осуществить во времени и пространстве эту сборку импульса его компоненты как раз и упорядочивают, производя чирпирование импульса и коллимацию пучка лучей, а затем уже пропускают через собирающий элемент (дисперсионную среду и линзу). Эта пространственно-временная аналогия проявляется и в уравнениях, описывающих изменение импульса в пространстве и времени.

    Так, рассмотрим импульс длительности Δt₀, испытавший в среде с нелинейностью квадратичную фазовую модуляцию Δφ(t)=sΔω₀t²/2Δt₀². Именно квадратичной будет модуляция фазы φ(t)~n₂I(t) в районе вершины гауссового импульса, которую можно приближённо аппроксимировать параболой (как легко убедиться, разложив профиль амплитуды или интенсивности импульса в ряд в окрестности вершины). А квадратичная фазовая модуляция эквивалентна линейной частотной модуляции

Δω(t)=dΔφ/dt=sΔω₀t/Δt₀²~dI/dt,                (3)

где s – знак частотной модуляции, Δω₀ – полное изменение частоты в пределах импульса. Тогда изменение длительности импульса будет описывать уравнение, напоминающее уравнение для описания изменения размера сфокусированного светового пучка [3, 4]:

Δt(z)=Δt₀[(1+sign(sβ₂)Δω₀Δt₀z/L_d)²+z²/L_d²]^1/2,                (4)

где L_d=Δt₀²/2|β₂| – длина дисперсионного расплывания. Это уравнение можно переписать в виде

Δt(z)=Δt₀[(1+2sβ₂Δω₀z/Δt₀)²+z²/L_d²]^1/2,                    (5)

откуда следует, что компрессия возможна при условии sβ₂<0. То есть, как было показано, чирпированный импульс, где частота повышается (s>0), для компрессии необходимо пропускать через среду с аномальной дисперсией (β₂<0). Либо наоборот, если удастся сгенерировать импульс с падением частоты (s<0), то его надо пропустить через среду с нормальной дисперсией (β₂>0). В итоге длительность импульса достигнет минимальной величины Δt_min=Δt₀/(1+M²)^1/2 на расстоянии, равном z_min=L_dM/(1+M²), где M=|Δω₀Δt₀| – параметр начальной частотной модуляции. Этот параметр компрессии достигает значений 10–100, что означает достижение степени сжатия импульса Δt₀/Δt_min≈M в десятки и сотни раз, то есть от пикосекундной до субпикосекундной и фемтосекундной длительности.

    В качестве нелинейной среды для чирпирования импульсов посредством фазовой самомодуляции оказывается удобно применять оптическое волокно, где нелинейные эффекты проявляются при меньшей интенсивности излучения. Ведь в волокне, где отсутствует дифракционная расходимость, и излучение всегда идёт в пределах тонкой сердцевины, диаметром в десятки микрон, высокая интенсивность излучения сохраняется вдоль всего волокна (протяжённостью в десятки метров), то есть велика эффективная длина нелинейного взаимодействия света со средой. Поэтому нелинейные эффекты накапливаются в течение всего времени движения вдоль этой длины и становятся весьма существенны, даже при умеренных интенсивностях излучения.

    Рассмотрим движение в такой нелинейной среде импульса гауссовой формы, с гауссовым профилем амплитуды

A=E₀exp(–t²/Δt₀²).                        (6)

    Нелинейная часть показателя преломления n₂I~n₂A²(t) вызывает нелинейный набег фазы

φ_nl=-n₂A²(t)zω₀/c.                        (7)

    Наибольшее изменение фазы наблюдается в вершине импульса при t=0 (Рис. 5), где φ_nl(0)=-n₂E₀²zω₀/c. Поскольку возле вершины импульса частота меняется почти линейно, то обусловленный фазовой самомодуляцией диапазон модуляции частоты можно выразить как Δω_nl≈φ_nl(0)/Δt₀~I(0)/Δt₀ – сдвиг частоты пропорционален скорости изменения интенсивности. Отсюда для параметра частотной модуляции можно получить простую формулу

M=|Δω_nlΔt₀|≈φ_nl(0).                        (8)

    Оценки показывают, что оптический импульс с пиковой интенсивностью I=(сn₀/8π)Е₀²=10⁹ Вт/см² изменяет показатель преломления в кварцевом волоконном световоде на величину n₂Е₀²=3,2∙10^–7. Если длина волны лазерного излучения λ₀=1 мкм, то 100-кратное уширение спектра можно получить в оптическом волокне длиной порядка 50 м.

    Самомодуляция фазы по гауссовому закону даёт линейный сдвиг частоты только в центральной части импульса (возле вершины, которая хорошо аппроксимируется параболой, а dI/dt, соответственно,– линейной функцией). Это вносит хроматические аберрации (аналогичные пространственным хроматическим аберрациям линз): огибающая импульса с такой частотной модуляцией заметно искажается при сжатии. Лучших результатов можно добиться, используя волоконный световод большей длины так, чтобы проявилась дисперсия групповых скоростей. В этом случае импульс немного уширяется, но при этом его вершина становится более плоской, а частотная модуляция становится почти линейной в пределах всего импульса (рис. 5.б). Такой импульс содержит 90 % энергии в центральном пике по сравнению с 68 % в бездисперсионном режиме самомодуляции (Рис. 5.а).

    Таким образом, в одном волокне часто совместно используют свойства нелинейного и дисперсионного элемента. Так, поскольку ряд волокон обладает аномальной дисперсией, то чирпирование и компрессия могут происходить в одном волокне, в котором чирп импульса, созданный нелинейностью, точно компенсируется аномальной дисперсией. Импульсы, подаваемые на вход такого волокна, сжимаются в солитоны, длительность и высота (пиковая интенсивность) которых определяются нелинейностью и дисперсией волокна. А сам импульс описывается нелинейным уравнением Гинзбурга-Ландау:

∂A/∂z=-αA/2-(β₁+iβ₂/2)∂²A/∂t²+iγ|A|²A,                     (9)

где A(z, t) – интенсивность светового поля E (медленно меняющаяся амплитуда огибающей импульса в зависимости от пути z вдоль волокна и времени t), α – постоянная затухания в волокне, β₁=dk/dω=1/V_g(ω₀) и β₂=d²k/dω² – коэффициенты разложения в ряд Тейлора волнового числа k (1), γ – коэффициент нелинейности. Как видно из уравнения (9), именно коэффициент β₂ позволяет скомпенсировать коэффициент нелинейности γ, дабы импульс, достигнув предельно малой длительности, перестал менять форму и протяжённость во времени. Это и позволяет оптическим солитонам двигаться в оптических волокнах, длительно сохраняя свою форму и малую протяжённость. А это весьма существенно для волоконно-оптических линий связи, в которых импульсы проходят сотни километров, на протяжении которых дисперсия и нелинейность, не будь они скомпенсированы, меняли бы сигнал до неузнаваемости, исключая передачу сигналов на такие расстояния.

    Таким образом, метод компрессии чирпированных импульсов не только позволяет достичь рекордно малой длительности импульса, но и долго удерживать этот рекорд, сохраняя на гигантских расстояниях форму и длительность импульса. Далее рассмотрим другие, менее известные способы компрессии импульсов.

    Как видим, основное ограничение по сокращению импульсов связано с тем, что импульс не может стать короче периода светового поля. Поэтому сам собой напрашивается вывод: надо сокращать длину огибающей импульса Δt при параллельном сокращении периода несущей T (Рис. 6). Такое пропорциональное сокращение импульса как целого можно осуществить, например, по эффекту Доплера, который увеличивает частоту излучения ν до величины

ν'=ν(1+V/c),                        (10)

если источник и приёмник сближаются со скоростью V. При этом не только пропорционально уменьшается период несущей T'=1/ν'=T/(1+V/c), но и во столько же раз уменьшается длительность импульса

Δt'=Δt/(1+V/c).                        (11)

    Фактически такое сокращение импульса опять же происходит за счёт применения линии задержки (на пути от источника к приёмнику), в которой передняя и задняя часть импульса оказываются в неравных условиях, проходят разный оптический путь: хвостовой части импульса, испущенной позднее, приходится проходить меньший путь, чем головной части импульса, поскольку расстояние между источником и приёмником сокращается. То есть работает общий принцип компрессии, по которому от такого неравных условий движения частей импульса он и сокращается. Причём в доплеровском случае импульс сжимается как целое, словно кузнечные мехи или мехи гармони, которые при сжатии сокращают и расстояния между соседними гребнями-складками. Так и при сжатии импульса в нём сжимаются и длины, периоды волн (Рис. 6). То есть в этом случае уже нет никаких принципиальных спектральных ограничений на возможную длительность импульса.

    Проще всего производить доплеровское преобразование частоты и длительности импульса по схеме А. Белопольского, передвигая не источник с приёмником, а зеркало, отражающее свет источника к приёмнику (Рис. 7). При этом исходная частота излучения источника ν воспринимается зеркалом, движущимся к источнику со скоростью V, на частоте ν'=ν(1+V/c), а затем переизлучается (отражается) колеблющимися свободными электронами зеркала и воспринимается приёмником на частоте ν''=ν'(1+V/c)=ν(1+V/c)². Такой эффект изменения частоты света после отражения от движущегося зеркала Белопольский впервые наблюдал в 1900 г., подтвердив тем самым справедливость эффекта Доплера в оптике [5, 6]. Однако изменение частоты получалось небольшим, ввиду малой скорости зеркал V в сравнении со скоростью света c. Как легко видеть, для того, чтобы компрессия импульсов по эффекту Доплера стала значительной, нужны скорости V, сопоставимые со скоростью света c. Поэтому в качестве зеркал-переизлучателей можно использовать движущиеся электронные сгустки. Под воздействием электромагнитной волны, испускаемой лазером, их электроны начинают колебаться и ретранслировать, переизлучать, направленно отражать свет, играя роль электронного зеркала, движущегося с околосветовой скоростью (Рис. 7).

    Подобный способ увеличения частоты лазерного излучения с пропорциональным сокращением периода световых колебаний и длительности импульса был действительно реализован на Стэнфордском линейном ускорителе SLAC, который разгонял электроны до энергий в 50 ГэВ [2]. Оптическое излучение лазера частоты ν~10¹⁵ Гц направлялось навстречу мчащемуся сгустку электронов и после отражения от него преобразовывалось в гамма-излучение частоты ν~10²⁵ Гц. Другими словами, частота несущей увеличивалась в 10¹⁰ раз, а значит длительность импульса сокращалась в 10 миллиардов раз! То есть, если исходная длительность импульса составляла порядка 10^–14 с (десятки фемтосекунд), то после сжатия должна была достичь 10^–24 с (порядка йоктосекунды). А это абсолютный рекорд. Конечно, такую длительность не могли измерить – для этого просто не существует приборов, к тому же исследователи интересовались лишь преобразованием частоты. Но такие короткие импульсы могут быть крайне интересны в плане исследования сверхбыстрых процессов, идущих в ходе превращения ядер и элементарных частиц.

    Казалось бы, электронный сгусток нельзя рассматривать строго как электронное зеркало, поскольку в отличие от зеркала он не плоский, а протяжённый и размытый. Однако на релятивистских скоростях ситуация меняется, и свет будет пересекать даже протяжённый сгусток за предельно короткое время, которое, подобно периоду световых колебаний снижено в огромное число раз (равное гамма-фактору), словно весь сгусток собран в одной плоскости (лоренцево сокращение), перпендикулярной вектору скорости сгустка. Поэтому отражение света от протяжённого сгустка можно рассматривать как отражение от плоского зеркала. Иногда такое отражение рассматривают как обратный эффект Комптона, при котором движущиеся электроны отдают свою энергию и импульс оптическим фотонам при столкновении, отчего их энергия растёт и они превращаются в энергичные фотоны рентгеновского и гамма-излучения [2]. При этом легко видеть, что направления движения отражённых фотонов будут практически совпадать (будучи параллельны направлению движения электронов), независимо от угла, под которым свет приходит к электронам. Вообще же, давно доказано, что обратный эффект Комптона полностью эквивалентен эффекту Доплера: происходит чисто классическое увеличение частоты при отражении, для объяснения которого квантовые гипотезы не обязательны.

    Поскольку мощный ускоритель есть не в каждой лаборатории, то желательно распространить этот метод на случай более медленных движений электронов. Это вполне возможно, если использовать многократное отражение, как в опыте Белопольского, который применил зеркала, движущиеся навстречу друг другу, отчего сдвиг частоты рос пропорционально числу отражений [6]. Поэтому, даже если применить сравнительно медленные электроны из электроннолучевых и рентгеновских трубок, где энергии электронов составляют порядка десятков кэВ, а скорости – десятые доли скорости света, то при многократном отражении можно добиться того же сжатия импульса, что и в мощном ускорителе, хотя и ценой потерь энергии при отражениях. Каждое отражение увеличивает частоту в (1+V/c) раз, так что частота на выходе из компрессора составит ν'=ν(1+V/c)ⁿ+1, где n – число отражений. Так при V=c/2 и при десяти отражениях (n=10) достигается уже почти стократное повышение частоты и стократное сжатие импульса Δt'=Δt/(1+V/c)ⁿ+1.

    При этом необходимо точно синхронизировать приход в одну точку электронных сгустков и лазерных импульсов. Кроме того, ввиду того, что скорости электронов в трубках уже не столь высоки, становится значимой форма электронных сгустков, которые должны иметь достаточно плоскую границу и высокую плотность, концентрацию электронов, чтобы увеличить коэффициент отражения. И то и другое достигается путём применения клистронов, которые, модулируя скорость электронного пучка, приводят к тому, что одни электроны догоняют другие, начинают группироваться, образуя уплотнения, электронные сгустки пучка (Рис. 19). Происходит своего рода компрессия электронного пучка, приводящая к сокращению его длины, повышению интенсивности (тока) и напоминающая компрессию оптического пучка, за счёт того, что электроны в сгустке, так же как лучи в оптическом импульсе движутся с разными скоростями. На некотором расстоянии это уплотнение достигает максимума: образуется почти плоское, тонкое и плотное скопление электронов, которое может служить отражающей границей. Лазерный луч должен успеть несколько раз отразиться между двумя такими границами, движущимися навстречу друг другу (Рис. 19). В итоге лазерный импульс, попавший меж этих двух стремительно сходящихся границ, оказывается как между молотом и наковальней, и сжимается вместе с длинами волн, подобно металлической заготовке.

    В свою очередь высокочастотное рентгеновское и гамма-излучение, созданное таким компрессором, можно использовать для ускорения электронов, выбиваемых под действием излучения из металла (фотоэффект). Чем выше частота ν' излучения, тем выше скорость и энергия hν' электронов, выбитых излучением. Эти электроны можно в свою очередь использовать для создания пучков и сгустков, на которых будет отражаться излучение, то есть организовать положительную обратную связь. Таким образом, генерируя всё более энергичные электроны, можно генерировать всё более высокочастотное и мощное излучение и всё сильней компрессировать лазерные импульсы. Следовательно, вполне возможно создать достаточно компактные и эффективные доплер-компрессоры импульсов. Причём степень сжатия импульса – коэффициент компрессии (отношение исходной длительности импульса к конечной длительности) уже не будет зависеть, как в чирп-компрессии от мощности излучения и свойств среды, а зависит лишь от скорости частиц, преобразующих импульс по эффекту Доплера.

    Как видели, наибольшую степень компрессии лазерных импульсов способны обеспечить те методы, в которых вместе с сокращением длительности импульса уменьшается период световых колебаний, растёт их частота. Такое изменение частоты происходит не только в эффекте Доплера, но и в других эффектах. В том числе это многочисленные нелинейные эффекты, например, эффект фазовой самомодуляции, эффект Рамана, генерация оптических гармоник. Однако во всех этих эффектах частота излучения меняется в лучшем случае в разы. А для рекордной компрессии необходимо сокращать период колебаний светового поля в сотни и тысячи раз. Существует ещё релятивистский эффект изменения частоты в ускоренно движущихся системах, выявленный с помощью эффекта Мёссбауэра [7]. Когда источник гамма-излучения частоты ν двигался с ускорением a, скажем при размещении его на крутящемся диске, при укреплении на вибрирующем пьезоэлементе, то приёмник, помещённый на расстоянии z, регистрировал излучение на изменённой частоте ν'=ν(1+az/c²). Как видно из формулы, эффект оказывается крайне мал из-за квадрата скорости света c в знаменателе. При обычных дистанциях z~1 м для изменения частоты в разы необходимы ускорения a~c²/z~10¹⁷ м/с², которые долгое время казались недостижимыми. И действительно, ни один излучающий прибор не может двигаться с таким гигантским ускорением. Однако элементарным излучателям – атомам и электронам такое ускорение придать вполне возможно.

    Например, в ускорителях, синхротронах электроны движутся с таким и даже ещё большим ускорением. Но даже и без этой сложной техники электронам или ионам легко придать требуемое ускорение. Действительно, из второго закона Ньютона в электрическом поле напряжённостью E ускорение электрона a=Ee/m (e/m=1,76·10¹¹ Кл/кг – удельный заряд электрона) достигнет нужной величины уже при E≈10⁶ В/м. Для ионов эта величина в тысячи раз больше: E≈10⁹ В/м. Такие напряжённости поля, и даже на порядки большие, легко достижимы. Так, если к обкладкам конденсатора, расположенным на расстоянии d=1 мм, приложить скромное напряжение U=1000 В (сравнимое с напряжением в бытовой электросети), то напряжённость электрического поля достигнет требуемой величины E=U/d=10⁶. А в сфокусированных лазерных пучках рекордной мощности амплитуда напряжённости переменного электрического поля достигает 10¹⁴ В/м [2], то есть на порядки больше требуемых значений. Не случайно такие мощные поля применяют для ускорения частиц, производя оптическое выпрямление – выделяя огибающую светового импульса, и ускоряя частицы полем плазменной волны, созданной лазерным импульсом.

    Кроме того, такие гигантские ускорения микрочастиц вполне достижимы под действием давления света высокой интенсивности. Так, даже при фокусировке непрерывного лазерного излучения с мощностью 1 Вт на шарик размером в микрон, тот приобретает под давлением света ускорение порядка 10⁷ м/с² [8]. Поэтому, если применить пикосекундные лазерные импульсы (длительностью порядка 10^–12 с), где за счёт концентрации света во времени достигают пиковых мощностей излучения вплоть до 10¹² Вт [8], то излучение, направленное на частицы меньших размеров (на ионы, атомы и наночастицы), вполне сможет сообщить им требуемое ускорение в 10¹⁷ м/с². Действительно, в современных лазерных установках могут быть достигнуты не только такие, но и на много порядков большие величины ускорений, вплоть до 10²³ м/с² [2]. Кроме того, как показано выше, электронам огромное ускорение придаёт поле плазменной волны, образованной лазерным импульсом. То есть компрессия импульсов указанным способом вполне реализуема. Всё, что необходимо сделать – это воздействовать лазерным излучением на свободные атомы или электроны, которые будут переизлучать свет на той же частоте за счёт томсоновского рассеяния. Если при этом заставить атомы и электроны двигаться с ускорением a~c²/z~10¹⁷ м/с², то можно существенно менять частоту излучаемого ими света и длительность импульсов.

    Каков же механизм изменения длительности и несущей частоты импульсов в ускоренно движущихся системах? Обычно его рассматривают в рамках общей теории относительности как аналогию эффекта замедления времени в поле тяготения, поскольку из общей теории относительности движение с ускорением эквивалентно действию поля тяготения. Классически этот эффект интерпретируют так: если фотон частоты ν и энергии W=hν от источника, расположенного на высоте z, падает на землю, то в поле тяготения он приобретает энергию mgz, где m=W/с² – масса фотона, g – ускорение свободного падения [9]. В итоге приёмник на земле воспримет излучение с частотой ν' и энергией

W'=hν'=hν+mgz=hν(1+gz/с²).                (13)

    То есть, зарегистрированная приёмником частота фотона ν'=ν(1+gz/с²) увеличится. А вместе с увеличением частоты света и уменьшением периода световых колебаний должна пропорционально сократиться и длительность импульса. По принципу эквивалентности общей теории относительности то же самое должно произойти и в системе, движущейся с ускорением a=g.

    Этому эффекту изменения частоты и длительности импульса при ускорении тоже можно дать чисто классическую интерпретацию, если рассматривать движение света как относительное, то есть, подобно Демокриту, Галилею и Ньютону, изучать полёт световых частиц и наделять их инерцией – способностью сохранять скорость, с которой они двигались вместе с источником. Как отмечал Вавилов, Галилея к мысли о том, что свет представляет собой механическое движение частиц, подтолкнуло наблюдение зажигательных зеркал Архимеда, которое доказывало, что частицы света движутся с огромной скоростью, и именно эта кинетическая энергия частиц выделяется при освещении, подобно разогреванию пуль, дробинок, попавших в мишень (по сути, подобное объяснение теперь предлагает и фотонная теория, представляющая свет в виде потока фотонов). Тогда, если источник движется к приёмнику с ускорением a, то есть скорость его сближения в каждый последующий момент времени увеличивается, то на ту же величину возрастает и скорость испущенного им света (изменение скорости света в вакууме под действием гравитации-ускорения не только допускают в общей теории относительности, но и напрямую фиксируют при радиолокации [10]).

    Благодаря этому лучи света и волновые фронты, испущенные источником позднее, догоняют испущенные ранее, сокращая дистанцию пропорционально пройденному пути z. При этом с одной стороны, как в эффекте фазовой самомодуляции, сокращается длина волны и повышается частота света ν'=ν(1+az/с²), а с другой – пропорционально сокращается длительность импульса Δt(z)=Δt₀ν/ν'≈Δt₀(1–az/с²). Отметим, что эта формула для преобразования частоты ускоренного источника была впервые получена в 1908 г. как раз в рамках классической интерпретации Вальтером Ритцем. И как раз такое изменение частоты было зафиксировано позднее в опытах с использованием эффекта Мёссбауэра, где источник двигался ускоренно [7]. Фактически, такой эффект компрессии тоже основан на применении линии задержки – пути z, на котором хвостовая часть импульса догоняет головную за счёт разницы скоростей. Такое инерционное сокращение волн, импульсов аналогично уплощению свинцовых пуль, пускаемых в тире. При ударе в мишень пуля затормаживается в головной части, тогда как задняя часть, продолжая двигаться по инерции, сжимает пулю в продольном направлении (пуля сплющивается под действием возникшего ускорения – тормозной перегрузки), одновременно расширяя в поперечном. Примерно то же происходит и с импульсом, который при сжатии пропорционально наращивает интенсивность.

    Рассмотрим данный эффект изменения частоты и периода световых колебаний количественно, на примере источника, излучающего световые сигналы через малый промежуток времени dt и расположенного от приёмника на расстоянии z. Свет, испущенный источником в момент времени t, достигнет приёмника в момент t'=t+z/c, где c – скорость света в вакууме. Малое время dt', протёкшее между приёмом двух световых сигналов, найдётся дифференцированием t' по t:

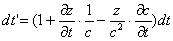.                        (14)

    При выводе данной формулы рассмотрен общий случай, при котором скорость света c играет роль не фундаментальной константы (как постулирует специальная теория относительности), а рассматривается в качестве переменной (как обычно делают в общей теории относительности). Такая переменность скорости света в вакууме была экспериментально обнаружена при космической радиолокации: при прохождении радиосигнала возле Солнца скорость радиосигнала снижалась и он приходил с запозданием, как было обнаружено в исследованиях И. Шапиро [10].

    В таком случае первое переменное слагаемое в скобках формулы (14) характеризует обычный эффект Доплера dt'=(1+V_z/c)dt, поскольку ∂z/∂t – это лучевая скорость V_z источника относительно приёмника (проекция скорости вдоль луча зрения). А второе слагаемое характеризует изменение периода сигналов за счёт изменения скорости света. Подобный эффект

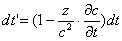,                        (15)

дополняющий доплеровский, экспериментально выявлен, как отмечалось, по эффекту Мёссбауэра [7]. Поскольку свет, летящий по инерции, ежесекундно снижает свою скорость с на величину ускорения a источника в направлении приёмника, то ∂с/∂t=a. Отсюда, после подстановки и получим формулу dt'=(1–az/с²)dt, с пропорциональным изменением периода световых колебаний T'=T(1–az/с²) и длительности импульса Δt(z)=Δt₀(1–az/с²). Соответственно частота меняется как

ν'=1/T'=ν/(1–az/с²)≈ν(1+az/с²).                (16)

    Как частное проявление эффекта, описываемого формулой (15), можно в принципе рассматривать и фазовую самомодуляцию, где тоже происходит изменение скорости света. Однако там вариация скорости света ∂с/∂t вызвана не ускорением источника, а нелинейными свойствами среды: неравенство фазовых скоростей вдоль импульса тоже приводит к сближению гребней волн и увеличению частоты света пропорционально пройденному пути z. Существенное отличие рассмотренного выше инерционного эффекта состоит в том, что такое неравенство скоростей проявляется и в вакууме, что весьма важно, поскольку позволяет безгранично повышать мощность и длительность импульса без риска повреждения, пробоя среды, а также непредсказуемых нелинейных изменений её свойств, ограничивающих возможности фазовой самомодуляции по преобразованию частоты импульса, скажем за счёт изменений его формы.

    Самое интересное, что в рассмотренном эффекте, так же как при компрессии по эффекту Доплера, степень сжатия может быть сколь угодно большой, поскольку вместе с импульсом сжимаются и длины волн, то есть для импульса нет спектральных ограничений. Минимальной длительности Δt(z)=Δt₀(1–az/с²)=0 импульс достигнет по прошествии пути z_min=с²/a. На таком расстоянии частота и интенсивность излучения стремятся к бесконечности, а длина волны – к нулю. При дальнейшем движении импульс снова начинает линейно уширяться, как в случае чирп-компрессии, с той только разницей, что в случае чирп-компрессии фокусировка не идеальная: длительность импульса ("временная перетяжка", Рис. 4) достигает конечной величины за счёт спектрального ограничения. Тогда как в случае компрессии по эффекту Ритца (15) достигается абсолютная фокусировка: длительность импульса спадает до нуля (Рис. 9), как если бы сфокусированный линзой пучок света имел бы форму идеального конуса и все лучи сходились бы точно в одной точке, а не формировали перетяжку конечной толщины за счёт дифракционного предела.

    Рассмотренный метод компрессии импульсов практически пока не исследован. Однако, вполне возможно, что подобный эффект сжатия импульсов уже давно наблюдается в генераторах аттосекундных импульсов, где как раз происходит компрессия исходного лазерного импульса длительностью в десятки-сотни фемтосекунд (10^–15 с) в импульс с длительностью в сотни аттосекунд (10^–18 с), с пропорциональным увеличением максимальной частоты, переходящей из оптического диапазона в рентгеновский. Такая компрессия происходит под воздействием мощного лазерного излучения на атомы инертного газа. Так что атомы как раз должны приобретать под действием светового давления гигантские ускорения a~10¹⁷ м/с², то есть при рассеянии лазерного света они вполне могут преобразовывать его по рассмотренному эффекту (16). Как правило, генерацию рентгеновского излучения и аттосекундных импульсов объясняют по более сложному механизму: излучение вначале ионизует атомы, отрывая от них электроны, затем электроны набирают в электромагнитном поле световой волны высокую энергию, а затем вновь поглощаются атомами, выделяя избыток энергии в виде излучения повышенной частоты [2]. Но не исключено, что параллельно работает и рассмотренный выше способ компрессии.

    Давление света на атомы газа было открыто ещё в 1907 г. П.Н. Лебедевым, который показал, что давление это растёт пропорционально интенсивности света. Поскольку в лазерном импульсе интенсивность меняется (рис. 11), то сначала давление на атомы и их ускорение a нарастает, достигает максимума, а затем спадает до нуля. Соответственно частота излучения ν'=ν(1+az/с²) сначала плавно нарастает до максимального значения, а затем так же плавно снижается. И действительно, как показывает анализ спектра (Рис. 10), в нём представлены все спектральные составляющие – от исходной оптической частоты ν и до максимальной ν', лежащей в рентгеновской области, причём интенсивности спектральных составляющих сопоставимы. Таким образом, вполне возможно, что рассмотренный метод компрессии давно уже реализован и успешно применяется, хотя об этом никто не подозревает.

    Не исключено, что подобный же эффект компрессии оптических импульсов реализуется и в космосе, где за счёт гигантских расстояний z преобразование частоты и длительности импульсов происходит при гораздо меньших ускорениях a~c²/z. Яркий пример – это рентгеновские пульсары. Так, пульсар в Крабовидной туманности тоже имеет очень широкий спектр излучения, простирающийся от радиодиапазона до оптического, рентгеновского и гамма-диапазона. При этом пульсар генерирует излучение в виде периодичных коротких импульсов, с длительностью и периодом в доли секунды, то есть с периодом совершенно нетипичным для космических процессов, где осевые и орбитальные периоды составляют часы, дни и годы. Поэтому вполне может быть, что пульсары – это обычные звёзды, звёзды-цефеиды, повышающие яркость оптического излучения с периодом в часы и дни. Однако если эти звёзды движутся по широким орбитам, проходя участки где ускорение a≈c²/z, то рассмотренный эффект будет преобразовывать оптическое излучение в импульсы рентгеновского и гамма-излучения, имеющие гораздо меньшую длительность и период повторения. С одной стороны, это объясняет спектр излучения рентгеновских пульсаров и вспышек барстеров по форме очень близкий к спектру излучения абсолютно чёрного тела, типичного для звёзд, но со спектральным максимумом сильно сдвинутым в высокочастотную область. С другой стороны в этом случае становятся излишними сложные и спорные объяснения пульсаров с привлечением искусственных гипотез о сверхплотных нейтронных звёздах, крутящихся с немыслимой частотой и генерирующих излучение по весьма надуманным механизмам.

    Одновременно за счёт сильной компрессии импульса по закону сохранения энергии должно происходить пропорциональное увеличение мощности излучения. Возможно, с таким повышением яркости мы сталкиваемся в случае новых и сверхновых звёзд, у которых как раз наблюдается сильное повышение яркости в течение очень короткого времени. Причём, чем короче вспышка, тем она ярче. Обычно эти вспышки интерпретируют как взрыв звезды, но новые и сверхновые вполне могут оказаться обычными звёздами, которые, двигаясь по широким орбитам, проходят положения, где их ускорение, направленное к наблюдателю составляет a≈c²/z, приводя к накоплению и компрессии излучения в виде яркой вспышки (это своего рода ударная световая волна, напоминающая ударную звуковую волну от сверхзвукового самолёта). Не случайно у ряда новых и новоподобных звёзд вспышки повторяются через некоторые характерные интервалы времени.

    Тот же эффект может приводить и к растяжению импульса, как в эспандере, если ускорение a будет направлено не к наблюдателю или приёмнику, а от него. Подобно тому как преобразование по эффекту Доплера dt'=(1+V_z/c)dt записывают через лучевую скорость V_z, эффект влияния ускорения можно записать в виде dt'=(1+a_zz/c²)dt, где a_z – лучевое ускорение, которое положительно, когда ускорение направлено от наблюдателя (т.е. в формуле (15) ∂с/∂t<0), и отрицательно, когда направлено к наблюдателю (отчего ∂с/∂t>0). То есть, когда ускорение источника a направлено от наблюдателя, регистрируемые им интервалы времени растягиваются dt'=(1+az/c²)dt, а частота снижается ν'=νdt/dt'≈ν(1–az/с²).

    Это опять же можно интерпретировать чисто классически, как отставание более поздних волновых фронтов, испускаемых источником с меньшей скоростью, чем вышедшие раньше. Поэтому задние фронты, испущенные с меньшей скоростью, отстают от передних, отчего, как при фазовой самомодуляции, в головной части импульса гребни световых волн расходятся, длины волн и периоды растут пропорционально пройденному пути (также это напоминает нелинейный эффект постепенного покраснения импульсов по мере их движения в волокне за счёт вынужденного комбинационного рассеяния, способного преобразовать оптическое излучение в ближний и средний инфракрасный диапазон). В космосе это будет приводить к увеличению длин волн, так что излучение будет смещаться в длинноволновую область спектра и преобразовываться из оптического в радиодиапазон. Этим можно объяснить не только мощное радиоизлучение квазаров и радиогалактик, но и покраснение света галактик пропорциональное расстоянию z до них и выражаемое законом Хаббла ν'=ν(1–Hz/с). Не случайно найденное из эффекта ν'=ν(1–az/с²) и известного ускорения a звёзд в галактиках значение постоянной Хаббла H=a/с получается близким к известному из наблюдений H=75 км/с/Мпк.

    Отметим, что именно такой эффект постепенного преобразования длины волны предполагал и сам Э. Хаббл (открывший закон красного смещения), и А. Белопольский, и К. Циолковский, которые отвергли гипотезу о том, что красное смещение в спектрах галактик вызвано расширением Вселенной. Да и пионер нелинейной оптики С.И. Вавилов писал в работе "О принципах спектрального преобразования света" [11]: "Можно ли считать это смещение также доплеровским, вызванным трудно постижимой рецессией туманностей, или же причина кроется в новых, неизвестных нам доселе свойствах света,– это вопрос открытый, который, может быть, несколько разъяснится после того, как начнёт функционировать пятиметровый рефлектор обсерватории Паломар в США. Хэббл, установивший самый факт и закон красного смещения, считает, что фотометрические данные не благоприятствуют интерпретации красного смещения как доплерова".

    Из слов Вавилова видно, что он допускал в качестве альтернативного объяснения красного смещения – некие неизвестные науке свойства света, позволяющие менять его частоту при движении света от галактик: "Единственным способом вариации частоты во всякого рода термодинамических мысленных опытах со времён В. Вина остаётся перемещение зеркал, меняющее частоту отражаемого света. Правда, этим дело не ограничивается; из наблюдений в космических масштабах мы теперь достоверно знаем о существовании загадочного универсального красного смещения в спектрах спиральных туманностей, возрастающего с расстоянием туманности от нас". При этом Вавилов подчёркивал, что в вакууме "единственной причиной изменения частоты света может быть только относительное движение источника и наблюдателя" и что "Во всяком случае нельзя забывать, что, изучая свет спиральных туманностей, мы имеем дело с лучами, не испытавшими никаких воздействий со стороны вещества в течение десятков и сотен миллионов лет и существовавшими без всяких воздействий в течение этих громадных периодов" [11].

    Более того, Вавилов экспериментально искал подобный эффект, хотя и отмечал, что: "Экспериментальные попытки (без каких-либо серьёзных опытных или теоретических оснований) влиять силовыми полями на частоту светового потока, начинающиеся с Фарадея и продолжающиеся до последнего времени, никакого положительного результата не дали". Последнюю попытку такого рода поиска Вавилов связывал как раз с возможностью изменения скорости света в вакууме и рассмотренным выше эффектом Ритца (15), предложив наблюдать трансформацию спектра света от быстро движущихся ионов при модулировании их скорости как раз посредством воздействия электрического поля на ионы. Однако Вавилов не успел поставить этот опыт [12].

    Характерно, что эффект, вызывающий красное смещение в спектрах галактик, вместе с периодом световых волн, растягивает также и видимую длительность процессов, в том числе длительность вспышек сверхновых. Так у галактик, в спектре которых наблюдалось двукратное увеличение длины волны света и периода световых колебаний, вспышки сверхновых были растянуты в два раза – с двух недель до четырёх недель. То есть данный эффект позволяет пропорционально растягивать длительность импульсов, работая как космический эспандер, что однако принято объяснять экспансией, расширением Вселенной.

    Таким образом, рассмотренный выше эффект может быть применён не только для компрессии и повышения частоты излучения, но и для растяжения импульсов и понижения частоты лазерного излучения, в том числе, для перевода оптического излучения лазера в ИК- и терагерцовый диапазон. Как видим, рассмотренный эффект одинаково проявляется и в микромире, и в космосе, и для атомов, и для звёзд, и позволяет связать воедино оптический диапазон со всеми остальными, открывая широкие возможности для трансформации лазерных импульсов. Далее рассмотрим технические реализации и особенности рассмотренных выше методов компрессии.

    Разберём конкретные устройства, применяемые для чирпирования и компрессии импульсов. Чтобы чирпировать исходный импульс, его пропускают через нелинейную среду. При этом стараются подобрать среду с высокой степенью нелинейности. Поскольку, чем выше нелинейность, тем при меньшей мощности излучения у импульса появится чирп. В этом случае идеальным решением оказывается оптическое волокно, в котором всё излучение идёт в тонкой сердцевине, часто имеющей поперечник в несколько микрон (Рис. 12).

    Напомним, что оптическое волокно (световод) представляет собой тонкую, толщиной в человеческий волос центральную жилу – сердцевину, обычно из кварцевого стекла с добавками, покрытую кварцевой оболочкой иного состава с меньшим показателем преломления. За счёт полного внутреннего отражения от границы сердцевины и оболочки, излучение распространяется внутри сердцевины, как в волноводе, что обычно иллюстрируют с помощью струи воды из бочки, в которую заведён луч света, идущий внутри струи, независимо от её изгибов. Так и свет в волокне распространяется в пределах тонкой сердцевины. Благодаря этому можно существенно увеличить длину нелинейного взаимодействия (то есть, оптический путь, в пределах которого за счёт повышенной интенсивности происходит нелинейное взаимодействие света с веществом). На этой длине и происходит нелинейное преобразование импульса: фактически это будет вся длина волокна.

    Если же фокусировать свет с помощью линз и зеркал, то удаётся обеспечить область перетяжки (самого узкого места пучка света) длиной не более долей сантиметра. Соответственно и длина нелинейного взаимодействия составляет примерно ту же величину, поскольку именно в перетяжке диаметром порядка микрон достигается экстремальная интенсивность светового поля, необходимая для создания нелинейных эффектов. Тогда как в волокне на всём его протяжении излучение собрано в такой узкой области, то есть имеет экстремальную интенсивность (Рис. 13). Соответственно нелинейные эффекты за счёт большой длины нелинейного взаимодействия проявляются при меньшей мощности излучения, которая не ведёт к перегреву и разрушению (оптическому пробою) нелинейной среды, нередко возникающему при фокусировании мощного излучения в толще материала.

    Несложный расчёт позволяет оценить минимальную мощность излучения P₀, необходимую для проявления нелинейных эффектов, включая эффект фазовой самомодуляции и генерацию солитонных импульсов: P₀=1/γL [3, с. 56]. Здесь L – длина световода, составляющая обычно несколько метров, γ – параметр нелинейности, связанный с нелинейным показателем преломления n₂ и составляющий обычно 1 Вт^-1км^-1. Отсюда P₀ порядка сотен Вт. Это огромная для волокна мощность, и, будь излучение непрерывным, волокно непременно расплавилось бы задолго до того, как удалось бы наблюдать нелинейные эффекты. Но за счёт работы в режиме ультракоротких импульсов, если их равномерно размазать по оси времени (Рис. 14), средняя мощность излучения P_ср будет обычно составлять порядка 100 мВт. Зато в пределах импульса мгновенная мощность окажется огромной P_M=P_срT_сл/Δt=20 кВт, где T_сл – период следования импульсов, составляющий обычно порядка T_сл=1/f=10^–8 c=10 нс (f – частота следования импульсов, которую можно найти по осциллографу, определяется временем обхода светом резонатора z_Σ/c и составляет обычно порядка f=100 МГц), а длительность импульса Δt порядка 10^-13 с. Как видим, за счёт малой длительности импульсов и их высокой скважности T_сл/Δt≈10⁵ в оптическом волокне удаётся создать гигантские пиковые мощности P_M>P₀, вполне достаточные для наблюдения нелинейных эффектов.

    После того как импульс успешно чирпирован, можно приступить к его компрессии в среде с аномальной дисперсией. Как говорилось, среды почти всегда имеют нормальную материальную дисперсию. Поэтому элементы с аномальной дисперсией приходится создавать искусственно. Рассмотрим, как это можно сделать. Материальная дисперсия связана с наличием в веществе характерных времён – периодов собственных колебаний электронов в атомах, отчего среда неодинаково откликается на излучение разных частот, и придаёт волнам неодинаковый фазовый сдвиг, по-разному меняет фазовую и групповую скорость волн. Поскольку характерные времена должны быть при этом порядка периода световых колебаний, то этот путь регуляции дисперсии слишком затруднителен: создание столь высокочастотных колебательных систем пока представляет большую сложность. Но есть другой механизм создания дисперсии – за счёт наличия в системе характерного пространственного масштаба или периода. Когда длина волны сопоставима с этим периодом, то система тоже неодинаково реагирует на движение волн разной частоты, пропуская их в разной степени и с разной скоростью, то есть порождает дисперсию. Если учесть, что в отличие от периода световых колебаний, длина световой волны имеет уже вполне ощутимый масштаб – порядка микрона, то есть тысячная доля миллиметра, то это позволяет легко создавать структуры с заданной дисперсией.

    Например, это может быть направляющая структура в виде волновода, в котором, как известно из электродинамики, скорость волн и дисперсия задаются уже не только материалом, материальной дисперсией среды, но, в первую очередь, формой и размерами сечения волновода. Именно поэтому оптический волновод – оптическое волокно с диаметром сердцевины порядка микронов позволяет, путём подбора этого диаметра и материала сердцевины, ответственного за материальную дисперсию, формировать необходимую дисперсионную кривую, в том числе обеспечить в некотором диапазоне частот аномальную дисперсию групповых скоростей. Чаще всего для создания аномальной дисперсии применяют одномодовое волокно SMF (Single Mode Fiber), где распространяющейся оказывается только одна мода. На рисунке 15 приведена его типичная дисперсионная характеристика. Точку, где дисперсия обращается в ноль, называют областью нулевой дисперсии. Как правило, работая в области аномальной дисперсии, стараются подобрать рабочую длину волны близко к нулевой дисперсии. С одной стороны это позволяет точней подобрать длину волокна, необходимую для компрессии – максимального сближения головной и хвостовой части импульса, поскольку, чем меньше дисперсия, тем больше компрессирующая длина волокна. С другой стороны, если компрессия импульсов происходит в солитонном режиме, то есть в одном волокне, где дисперсия и нелинейность компенсируют друг друга, то в районе нулевой дисперсии лучше работать потому, что там должна быть мала и нелинейность, а это необходимо, чтобы избежать ненужных нелинейных преобразований формы солитона и распада солитона на солитоны меньшего порядка за счёт распадной неустойчивости.

    Волокно с аномальной дисперсией часто бывает необходимо ещё и в качестве компенсатора дисперсии, поскольку активное волокно, легированное (допированое) активными ионами (например, ионами эрбия Er³⁺), где происходит усиление импульса, как правило, имеет нормальную дисперсию, то есть ведёт к расплыванию, уширению импульса, которое необходимо скомпенсировать. Этой цели и служит волокно с аномальной дисперсией. Длину этого волокна обычно подбирают как раз из условия, чтобы оно компенсировало нормальную дисперсию активного волокна и других оптических элементов системы. Пользуясь уравнением (4) расплывания-сжатия импульса в среде с нормальной и аномальной дисперсией, находят, при каком условии длительность импульса достигает наименьшего значения. Из этого условия теоретически рассчитывают требуемую длину волокна. После чего, приварив волокно с длиной, немного превышающей расчётную, наблюдают с помощью автокоррелятора, какой получается длительность импульса, и постепенно отрезают небольшие куски волокна, добиваясь того, чтобы длительность импульса стала предельно малой.

    Схема волоконного лазера с компрессией чирпированных импульсов представлена на Рис. 14. Типичная схема подобного лазера, устроенного по кольцевой схеме показана на Рис. 16. Так же как в лазерах с кольцевым резонатором, лазерный импульс бегает по кольцу (по часовой стрелке) из сваренных вместе оптических волокон, на каждом пробеге усиливаясь в активном волокне и сжимаясь в волокне SMF. В качестве накачки служит излучение лазерного диода на длине волны 0,98 мкм, заводимое в активный световод (легированный, допированный ионами эрбия) через WDM-каплер (wavelength division multiplexion), осуществляющий сведение, сдваивание световых потоков. Таким образом, в волоконных световодах в качестве активной среды используют само оптическое волокно, его кварцевую сердцевину, в которую как в матрицу внедрены активные центры – ионы металлов. Рабочие переходы между уровнями этих ионов как раз и задают частоту лазерного излучения.

    Обычно в качестве активных применяют ионы переходных металлов – элементы Iб–VIIIб подгрупп таблицы Менделеева, имеющие незаполненные внутренние электронные оболочки, наиболее богатые необходимыми переходами и метастабильными уровнями. В первую очередь это титан, хром, ряд редкоземельных металлов (например, неодим, эрбий, тулий…, соответственно лазер называют неодимовым, эрбиевым, тулиевым).

    К отрезку активного световода-усилителя (У346) длиной в 3 м приварен кусок световода SMF длиной в 5 м, имеющего на длине волны 1,56 мкм аномальную дисперсию, которая компенсирует нормальную дисперсию активного световода (мешая расплыванию импульса), осуществляет компрессию импульсов и работу лазера в солитонном режиме, когда дисперсия скомпенсирована нелинейностью.

    Генерируемое излучение выводится через второй WDM-каплер. Выходной сплавной каплер – контакт выходного световода с участком кольцевого световода,– позволяет выводить часть энергии сформированного лазерного импульса из системы. Естественно поэтому, что частота повторения импульсов просто равна времени обхода светом кольцевого резонатора волоконного лазера. Отчасти каплеры аналогичны полупрозрачным зеркалам резонаторов обычных газовых или твердотельных лазеров. Для обеспечения однонаправленного движения импульсов в волокне система содержит изолятор Фарадея, представляющий собой гиротропный элемент (например, железо-иттриевый гранат) с установленными по краям поляризаторами, что и обеспечивает движение импульсов по кольцу лишь в одном заданном направлении (по часовой стрелке).

    Генерация ультракоротких пикосекундных и фемтосекундных импульсов основана на методе синхронизации мод с помощью насыщающегося поглотителя. Роль такого поглотителя играют скрещенные поляризаторы в изоляторе Фарадея, дополненные поляризационными контроллерами ("ушами"), представляющими собой свёрнутые в катушки участки волокна, которые можно поворачивать. Они аналогичны по действию пластинкам λ/2 и λ/4 (вносящим фазовый сдвиг между перпендикулярными компонентами поля, соответственно на π и π/2), поскольку изгиб волокна вызывает двулучепреломление за счёт разницы показателей преломления для лучей с колебаниями электрического поля вдоль и поперёк плоскости изгиба (плоскости катушки). Благодаря этому исходное излучение удаётся преобразовать в линейно-поляризованное, которое при попадании на поляризатор в изоляторе Фарадея гасится почти до нуля при обычных интенсивностях света. Но при высоких лазерных интенсивностях, за счёт эффекта насыщения наступает просветление поглотителя и мощное излучение, возникающее в случае ультракоротких импульсов с гигантской пиковой мощностью и интенсивностью, прорывается через поглотитель. С точки зрения теории колебаний это происходит, когда все моды лазера оказываются засинхронизованы по фазе, то есть горбы синусоид нескольких миллионов мод складываются в фазе в момент просветления [2]. Такой постепенный процесс синхронизации мод, происходящий спонтанно и нарастающий с течением времени с каждым проходом через поглотитель, можно рассмотреть и с точки зрения теории колебаний, изучающей взаимодействие мод за счёт нелинейной связи, осуществляемой как раз насыщающимся поглотителем. Такой же поляризационный контроллер установлен на выходе изолятора Фарадея.

    Таким образом, методы модуляции добротности и синхронизации мод тоже можно рассматривать как своего рода методы компрессии лазерных импульсов, поскольку с их помощью сравнительно широкие лазерные импульсы сжимаются в короткие и ультракороткие за счёт того, что беспорядочно движущиеся пространственные и частотные составляющие импульса, собираются вместе, компрессируются, формируя короткий и мощный импульс. Правда, компрессия эта происходит ещё внутри лазерного резонатора. Точно так же и сам лазерный генератор можно рассматривать как своеобразный компрессор непрерывного излучения накачки в отдельные импульсы, отчего их пиковая мощность пропорционально нарастает.

    Широко применяемая в лазерных оптоволоконных схемах диодная накачка особенно удобна и эффективна, поскольку почти всё излучение накачки, собранное в волокне, доходит по назначению и длительно взаимодействует с активными центрами, распределёнными вдоль активного волокна. При этом накачка в волокне может быть как попутной (излучение накачки идёт в том же направлении, что и лазерное излучение, Рис. 14) и встречной (излучение накачки идёт навстречу лазерному, Рис. 16). Последняя схема более эффективна, поскольку инверсия населённостей уровней активных атомов "выедается" тем скорее, чем выше интенсивность лазерного излучения. Поэтому для эффективной и более равномерной накачки вдоль волокна необходимо, чтобы по мере распространения и усиления лазерного импульса в активном световоде, концентрация атомов с инверсией населённостей нарастала, что и обеспечивает встречная накачка.

    Также существуют волоконные лазеры, устроенные по обычной схеме двузеркального резонатора, где свет лазера бегает не по кольцу в одну сторону, а отражается между двумя зеркалами, установленными на противоположным концах волокна. В качестве зеркал при этом обычно используют брэгговские диэлектрические зеркала, то есть отражение происходит от периодичной структуры (её период равен половине длины волны), сформированной за счёт неоднородности показателя преломления волокна. Поскольку ультракороткие импульсы имеют широкий спектр, то период приходится делать постепенно меняющимся вдоль волокна, чтобы оно отражало все длины волн – одни раньше, другие – позднее. Такой отражательный элемент, кроме всего прочего, можно также использовать и для создания аномальной дисперсии, поскольку излучение разных частот проходит разный путь до места отражения и длина резонатора для них оказывается разной. Линейная схема также содержит активный световод-усилитель и световод, служащий нелинейным элементом, компрессором и компенсатором дисперсии (Рис. 14).

    Соединение оптических волокон, имеющих диаметры в сотни микрон и центральные жилы диаметром в микроны – это прецизионная и наиболее ответственная операция, поскольку от того, насколько точно состыкованы волокна, насколько соосны их центральные жилы (по которым распространяется свет), сильно зависят потери светового потока в месте стыка. Небольшой дефект, пылинка, малейшая неровность или несоосность сводят всю работу насмарку, делая стык волокон непригодным. Вот почему "подковать" к круглому торцу одного световода (в человеческий волос толщиной) круглый торец второго световода – это операция, сопоставимая по уровню сложности с задачей тульского Левши, который подковал к лапкам блохи микроподковы. К счастью, сейчас эта операция во многом автоматизирована и производится своего рода механизированной микрокузницей – особым сварочным аппаратом, в захваты которого заправляют специально подготовленные концы двух волокон. В зависимости от типа волокон и заданного режима сварки, автомат сам юстирует углы волокон, их соосность, сам сводит их вместе и после разогрева электрической дугой (дугой В.В. Петрова) сваривает, "сковывает" волокна, а затем и проверяет качество сварки. Всю операцию можно даже наблюдать на экране встроенного "мелкоскопа".

    Рассмотренные схемы оптических волоконных лазеров очень удобны за счёт своей простоты, малого энергопотребления, компактности (волоконный лазер, собранный по кольцевой или линейной схеме, можно свернуть в небольшую катушку). Во многом этому способствует использование диодной накачки, поскольку лазерные диоды малогабаритны и эффективны, особенно при накачке в волокно. Отметим, что история светоизлучающих и лазерных диодов началась с Нижнего Новгорода, где в колыбели советского радио – нижегородской радиолаборатории, известный радиотехник О.В. Лосев ещё в 1920-х гг. впервые обнаружил эффект излучения света полупроводниками и эффект усиления при пропускании тока через полупроводники. Дальнейший прогресс в области создания светоизлучающих и лазерных диодов был связан с работами Н.Г. Басова, впервые выдвинувшего идею полупроводникового лазера, и с работами Ж.И. Алфёрова, идея которого о гетероструктурных полупроводниковых переходах как раз и позволила построить первый полупроводниковый лазер, который в свою очередь открыл широкий путь для развития волоконных лазеров.

    Компрессию чирпированных импульсов можно организовать и в лазере с обычными оптическими элементами – зеркалами и линзами. Здесь тоже возникает проблема, как создать компрессирующий элемент с аномальной дисперсией. И снова для создания дисперсионного элемента можно применить структуры с характерным периодом, который будет неодинаково воздействовать на волны разной длины. Таким элементом является, например, дифракционная решётка, которая, подобно призме, разлагает белый свет на спектральные составляющие – лучи разных цветов (частот) за счёт наличия характерного пространственного периода – параллельных штрихов, разделённых стандартными интервалами порядка микронов, что сопоставимо с длиной волны света. Это позволяет создать элемент с аномальной дисперсией, поскольку после разделения лучи можно заставить пройти разное расстояние, то есть накопить разность хода, а затем снова собрать их в параллельный пучок с помощью дифракционной решётки и, отразив глухим зеркалом, снова собрать в единый пучок. Подбирая дифракционные решётки, расстояния меж ними и углы их поворота, можно создать элемент с требуемой аномальной дисперсией (Рис. 18).

    Впрочем, даже в таком компрессоре в качестве нелинейной среды, производящей фазовую самомодуляцию, применяют обычно световод – либо обычное оптическое волокно, либо полый стеклянный капилляр, заполненный в качестве нелинейной среды инертным газом [2]. Лазерное излучение заводится в световод с помощью линзы под малым углом к оси световода, дабы обеспечить за счёт скользящего падения почти полное отражение, практически без потерь при многократных отражениях. Поперечник такого капилляра составляет порядка сотни микрон, а потому излучение в капилляре имеет высокую интенсивность, достаточную для нелинейного преобразования света по эффекту фазовой самомодуляции. Таким образом, компрессия чирпированных импульсов является одним из самых удобных и распространённых методов компрессии.

    Метод доплер-компрессии пока ещё малоисследован, не разработан и редко применяется, в первую очередь, из-за его сложности и необходимости разгонять электроны до релятивистских и ультрарелятивистских скоростей, для чего обычно требуется громоздкая высоковольтная или ускорительная техника (которая, тем не менее, находит всё более широкое применение в лазерной технике, скажем в лазерах на свободных электронах). И всё же, когда возможности чирп-компрессии будут исчерпаны и, упёршись в фундаментальный предел спектрально ограниченных импульсов, физики захотят сжимать импульсы до ещё меньших длительностей, им не обойтись без компрессии посредством сокращения длины волны и увеличения частоты несущей.

    Кроме того, стремление повысить интенсивность излучения, которая пропорциональна мощности излучения и обратно пропорциональна площади фокального пятна, тоже неизбежно заставит после достижения мощностного предела, сокращать размер фокального пятна, что невозможно сделать без сокращения рабочей длины волны: поскольку минимальная площадь пятна составляет порядка квадрата длины волны. То есть опять же не обойтись без компрессии импульса как целого, посредством эффекта Доплера. Как говорилось, здесь нет принципиальных ограничений по степени сжатия, и такая компрессия представляет собой чисто техническую задачу.

    Прежде всего, требуется точно синхронизовать движение сгустков частиц и лазерных импульсов, которые изменяют свою длительность и частоту излучения при рассеянии на сгустках. Характерные частоты прихода сгустков в ускорителях и накопителях составляют порядка десятков мегагерц. Примерно тот же порядок частот характерен для прихода лазерных импульсов, циркуляция которых по кольцу резонатора имеет много общего с циркуляцией электронных сгустков в кольце синхротрона и электронного накопителя. Период обоих процессов задан временем обхода ускорительного кольца и резонатора, соответственно, сгустками частиц и светом. Поскольку длины ускорительных колец и колец резонатора исчисляются метрами и десятками метров, а скорости релятивистских частиц – порядка скорости света, то и период повторения обоих процессов оказывается одного порядка. Поэтому, если подобрать соответствующую длину лазерного резонатора, волоконного кольца (её легко сделать регулируемой), то можно добиться точной синхронности импульсов лазера и прихода электронных сгустков. Та же ситуация, если использовать линейный ускоритель и лазер, собранный по линейной схеме.

    Поскольку ультрарелятивистский электронный сгусток, имеющий протяжённость порядка сантиметров, пролетает область взаимодействия с излучением за время порядка пикосекунд, то необходимо, чтобы, во-первых, лазерный импульс имел длительность не выше этой, а во-вторых, чтобы он поступал к сгустку точно в момент его пролёта через область взаимодействия. Таким образом, кроме точного равенства частот, необходимо ещё обеспечить фазу прихода импульса к пучку. Для этого можно либо менять путь лазерного пучка до точки взаимодействия, либо управлять фазой лазерных импульсов путём внешней синхронизации через оптический затвор, управляемый напряжением с ускорительного резонатора. Применение ультракоротких импульсов, полученных методом синхронизации мод, как раз и позволило добиться такой точной синхронизации и эффективного взаимодействия лазерных импульсов со сгустками частиц [2].

    Другой способ, как показано выше, состоит в применении электронных пучков, имеющих менее высокую скорость и образующих при фазовой фокусировке "электронные зеркала", движущиеся с той же скоростью. При многократном отражении от таких "зеркал" (Рис. 19), можно заметно уменьшить длительность импульса и длину волны несущей даже при умеренных и обычных релятивистских скоростях электронов. Здесь тоже основную роль играет синхронизация – совпадение частоты f модуляции электронного пучка в клистроне с частотой f генерации лазерных импульсов и обеспечение требуемой фазы прихода лазерных импульсов, которые должны приходить к "электронному зеркалу" точно в момент его формирования, когда сгусток имеет предельно малую толщину и максимальную плотность.

    Также можно избежать применения громоздких ускорителей, если использовать лазерные ускорительные системы – "настольные ускорители", позволяющие ускорять электроны и другие частицы полем световой волны за счёт давления света и нелинейных эффектов (выпрямления света, многофотонной ионизации и т.п.). Так, электроны можно ускорять в созданных лазерным импульсом нелинейных плазменных волнах до энергий порядка нескольких ГэВ, что вполне достаточно для преобразования импульса по эффекту Доплера. При этом основной импульс, воздействуя силой Лоренца на электроны, выталкивает их из газовой струи, формируя плазменную волну. Эта плазменная волна, движущаяся вслед за лазерным импульсом, и разгоняет электроны своим полем – так называемое кильватерное ускорение (поскольку сила действует аналогично силе, помогающей дельфинам плыть в кильватерной волне за кораблём). Уже сейчас таким способом достигнуты энергии электронов 50 МэВ при разгоне на длине в 1 мм [2], что, конечно, не сравнить со стометровыми и километровыми габаритами мощных циклических и линейных ускорителей. Таким образом, возможности лазерной ускорительной техники увеличиваются и открывают дополнительные возможность для преобразования и компрессии импульсов лазерного излучения.

    Инерционная компрессия с помощью ускорения – это ещё менее разработанный метод, чем доплеровская компрессия. Однако этот метод наиболее перспективен, поскольку позволяет сжимать длительность импульсов и повышать частоту несущей без разгона частиц до околосветовых скоростей. А значит, можно обойтись более простым оборудованием и меньшим расходом энергии, производя компрессию с высоким КПД. Ведь в рассмотренном методе существенным оказывается ускорение излучающих частиц, а не их скорость, как в эффекте Доплера. Если учесть, что ускорение должно составлять величину a~10¹⁷ м/с², то скорость, которую успеют набрать частицы за время воздействия лазерного импульса t=10^–14 с составит V=at=10³ м/с, то есть весьма умеренную скорость, сравнимую с тепловой скоростью атомов.

    Так же, как в случае доплер-компрессии, главное условие для инерционной компрессии – это точная синхронизация моментов ускорения частиц с моментами прихода к ним лазерного импульса. В том случае, когда ускорение вызвано световым давлением лазерного импульса, синхронизация происходит автоматически: частицы движутся ускоренно, пока на них действует давление света. Причём выше всего ускорение в момент наивысшей интенсивности излучения. Так, современные генераторы аттосекундных импульсов имеют сравнительно простое устройство: в вакуумированном объёме струя инертного газа истекает в вакуум, затем на ней фокусируется излучение в виде ультракоротких фемтосекундных лазерных импульсов, которые преобразуются в аттосекундные (рис. 10). Обратим внимание на важность вакуума – он гарантирует, что энергия импульса не расходуется на поглощение, ионизацию воздуха. Кроме того, исключается переизлучение света неподвижными атомами, которые не имеют ускорений, отчего переизлучённый ими свет перестаёт менять свою скорость и перестаёт преобразовываться.

    Недостатком такого метода является то, что в импульсе от изменения интенсивности излучения во времени меняется и ускорение атомов (Рис. 11). А потому разные части импульса сжимаются в разной степени: пьедестал импульса, где интенсивность излучения мала, практически не сжимается. Поэтому, строго говоря, импульс сохраняет прежнюю длину, и лишь обостряется – сжимается его вершина (примерно то же происходит при чирп-компрессии, поскольку линейная модуляция частоты возникает только возле вершины импульса), которая действительно может быть сокращена до аттосекундной длительности. Поскольку при этом существенно повышается мощность излучения, пьедестал просто перестаёт различаться на её фоне.

    Если же необходимо все части импульса сжать пропорционально, одинаково, сократив импульс до длительности Δt'=Δt(1–az/с²), и получить монохроматическое излучение на частоте ν'=ν/(1–az/с²), то нужно обеспечить постоянное ускорение частиц, на которых происходит рассеяние импульса. Как говорилось, проще всего этого добиться, налагая на частицы (электроны или ионы) сильное электрическое поле. После прохождения импульса поле можно снять, чтоб не тратить энергию на дальнейший разгон частиц. Это позволяет налагать поле импульсами, которые, во-первых, должны быть синхронны с импульсами лазера, а во-вторых, их длительность должна быть чуть больше длительности лазерного импульса, то есть составлять от 10^–12 до 10^–9 с. Малая длительность импульса не только уменьшает расход электроэнергии, но и позволяет создавать рекордные напряжённости поля простыми средствами, скажем, в искровом разряднике, путём резкого разрыва цепи, путём применения трансформатора Теслы и т.д.

    Отметим, что именно искровой разрядник позволил Г. Герцу впервые создать в 1888 г. электрические импульсы рекордно малых длительностей, периодов и высокой частоты повторения (порядка ГГц), когда ещё не было высокочастотных генераторов. Благодаря этому Герц и сумел впервые сгенерировать радиоволны, подтвердив электромагнитную природу света. Поскольку рекордное поле требуется создавать в течение очень малого времени, которое меньше времени, необходимого для начала разряда, то появляется возможность создавать в таком динамическом режиме рекордные напряжённости поля, которые превышают критические, ведущие к пробою.

    Таким образом, инерционный компрессор импульсов должен представлять собой вакуумированный баллон (Рис. 20), в который через окно-линзу заводится исходное излучение лазера, проходящее затем через прозрачный электрод (такие электроды есть, например, в жидкокристаллических экранах, и могут быть выполнены из разных материалов, устойчивых к мощному излучению, в том числе из графена), фокусируется на потоке электронов или ионов, эмитируемых с дополнительного электрода, к которому, так же как к первому приложено постоянное или переменное напряжение (синхронное с частотой повторения импульсов). После рассеяния на электронах или ионах, ускоренных электрическим полем, излучение выходит через второй электрод, имеющий отверстие или выполненный в виде сетки. После чего на пути свободного пролёта z, импульс преобразуется по эффекту (15), (16), сокращая свою длительность Δt'=Δt(1–az/с²) и повышая частоту несущей ν'=ν/(1–az/с²), после чего выходит через второе окно компрессора. Степень сжатия импульса можно регулировать путём изменения величины и направления ускоряющего поля E, то есть изменением ускорения a, или меняя длину свободного пролёта z до подвижной переизлучающей пластины, гасящей неравенство скоростей у лучей света.

    Поскольку электроды плоские и поле между ними – это, по сути, поле плоского конденсатора, то поле получается достаточно однородным, что необходимо для получения всеми электронами одинаковых ускорений для одинакового преобразования частоты.

Высокие поля E можно получить и путём миниатюризации электродов (Рис. 21). Так, возле острия с радиусом закругления r порядка микрона (10^–6 м) напряжённость поля E~U/r достигает значений E~10⁶ В/м уже при напряжении U=1 В. То есть трансформатор частоты может работать от простой батарейки, если фокусировать свет лазера точно перед остриём, окружённым электронами. Само остриё может служить эффективным источником электронов и ионов за счёт автоэлектронной, автоионной и холодной эмиссии, а также под действием освещения лазерным светом. Применение электрода в виде острия позволит также выполнить второй электрод в виде цилиндра, вместо электрода с отверстием или в виде сетки, который мог бы вызвать эффект переизлучения и тем самым нейтрализовать инерционное преобразование импульса.

    Можно преобразовывать рассмотренным способом и непрерывное излучение возбуждённых ионов, налагая на них мощное электрическое поле. Интересно, что установку, подобную рассмотренным выше схемам (Рис. 20, 21) ещё в 1950 г. планировал и С.И. Вавилов, стремясь проверить рассмотренный выше эффект преобразования частоты и переменность скорости света. Только в качестве ускоренных источников света он предлагал использовать не электроны, рассеивающие излучение лазера, а ионы, излучающие узкие спектральные линии (каналовые лучи), движущиеся в быстроменяющемся поле, которое, меняя скорость и ускорение частиц, позволяло бы выявить нелинейное преобразование частоты света на некоторой пролётной дистанции. Другими словами, Вавилов, предполагал обнаружить эффект, аналогичный клистронному, только для света, скорость лучей которого модулировалась переменным электрическим полем, так же как скорость электронов – в клистроне. Но, как говорилось, Вавилов так и не успел осуществить этот опыт [12].

    Итак, существует ряд простых способов реализации инерционной компрессии импульсов, и только будущее покажет, какой из них самый простой и эффективный.

    Среди рассмотренных методов компрессии есть как широко распространённые и хорошо изученные, так и совсем новые, почти не апробированные и почти неизвестные. Нет сомнений, что в ближайшие годы все эти методы будут находить всё более широкие и значимые применения, в науке, технике и жизни. Пока компрессоры лазерных импульсов существуют в основном в виде лабораторных прототипов, или в виде отдельных узлов лазерных установок, производимых промышленностью. Но со временем их, вероятно, станут изготавливать в виде отдельных агрегатов, которые будут способны сжимать любые лазерные импульсы, с произвольными характеристиками, до любой заданной длительности. Эти универсальные трансформаторы лазерных импульсов будут напоминать электрические трансформаторы и механические редукторы, которые можно произвольно присоединять к разным устройствам для соответствующего преобразования входного "сигнала".

    Это позволит существенно расширить область применения современных лазеров, охватить не только область медицины, измерительно-диагностирующей аппаратуры, военной техники, но и поспособствует созданию новых ускорителей, ракетных двигателей и открытию многих других неожиданных областей применения. Большинство современных лазеров, рассчитанных на разные диапазоны, можно будет заменить одним наиболее простым и экономичным, дополнив его трансформатором импульсов, который будет по желанию преобразовывать длительность и частоту излучения. Но главное, трансформаторы импульсов, производящие компрессию, позволят получить импульсы рекордно малых длительностей и пространственных размеров для прецизионной обработки деталей микро- и нано-габаритов [2]. Так, у сфокусированных фемтосекундных импульсов не только ширина, но и длина составляет порядка микрона. Такие компактные импульсы, называемые "световыми пулями", позволяют не только производить прецизионную обработку деталей, посредством "обстрела пулями", но и проводить прецизионные измерения во временной и пространственной области по принципу лидаров (лазерных радаров), точность которых определяется длительностью импульса, составляя микроны и фемтосекунды. Вдобавок компрессия позволяет достичь рекордной мощности и интенсивности, в том числе для изучения совершенно неизвестных свойств вещества и поведения материалов, атомов и элементарных частиц в экстремальных оптических полях.

    Подобно тому, как кузнец по желанию трансформирует форму, свойства и структуру металла, превращает с помощью огня и молота бесформенную заготовку в виде куска железа в полезные вещи, с разными назначениями, от военных до вполне мирных, так и физик, вооружённый компрессором, с помощью нелинейности и дисперсии, электричества и инерции, придаёт одному и тому же простому лазерному импульсу самые разные свойства и практически значимые применения. Как легендарный тульский кузнец Левша, так и физик с помощью методов компрессии всё дальше проникает в мир рекордно малых размеров и длительностей, так что с помощью лазера теперь не проблема изготовить и подковать блоху не только микро-, но и наноразмеров [2, с. 157]. Не зря наш физик-электротехник А.Н. Лодыгин (изобретатель электролампы, акваланга, вертолёта и вероятный прообраз жюль-верновского капитана Немо и Робура-Завоевателя), принёсший людям электрический свет,– первую лампу накаливания с тончайшей угольной и вольфрамовой нитью, начинал свой путь в науку из кузниц, с тульских оружейных заводов, где работал кузнецом, молотобойцем, слесарем. Именно там, за обработкой нагретых до белого каления металлических заготовок, он пришёл впервые к идее ламп накаливания и ковки тончайших светоизлучающих волокон (их спирали ныне изготавливают методом волочения через тончайшие алмазные фильеры). Этими первыми лампами он удивил за рубежом многих, включая предприимчивого американца Эдисона.

Дата установки: 21.07.2012
[вернуться к содержанию сайта]

W