

Кто из нас не мечтал иметь санки, которые, съехав с горы, как по щучьему веленью, сами б взбирались наверх. Но, оказывается, катки, способные въезжать в горку, всё же бывают. Впервые такой каток я увидел в зале занимательной науки музея нижегородской радиолаборатории, что на набережной, в красивой демонстрации инженера С.А. Гилёва. И хотя прежде был наслышан о чудо-катке, увидеть его в действии странно. Когда на ваших глазах один каток съезжает с горки, а другой в неё же забирается, то нельзя не подивиться. А меж тем и катки и горка устроены предельно просто. Каток – это выточенный из оргстекла биконус – два одинаковых конуса, сложенных основанием, а горка – две одинаковых скошенных рейки, ребром поставленные на стол под углом друг к другу. В зависимости от этого угла и угла скоса реек, каток, поставленный на рейки, словно на рельсы, либо скатится, либо въедет в горку, а может и остаться на месте. Не имея опыта, трудно угадать, как он себя поведёт.
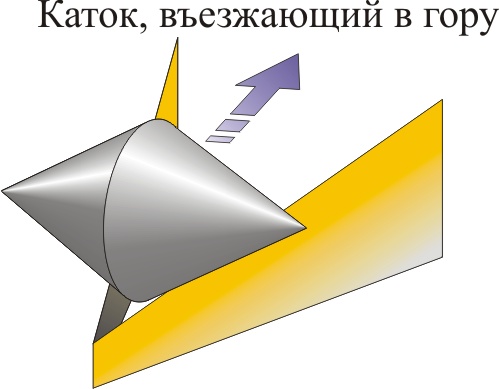
Эту нехитрую установку можно собрать и дома. Каток легко сделать из двух одинаковых пластиковых бутылок, срезав у них конические верхушки, которые потом скрепляются клеем либо трубкой, пропущенной через горлышки. А две деревянных рейки можно заменить вырезанными из картона. Каток поменьше можно собрать из двух навинчивающихся наконечников от гелевых ручек. Их конусы тоже можно склеить или свинтить в биконус. Когда читатель поэкспериментирует с собранной установкой, меняя катки и углы реек, у него могут возникнуть два вопроса. Во-первых, почему каток способен как скатываться, так и заезжать в горку? А во-вторых, как найти то переломное, критическое соотношение параметров установки, по достижении которого каток, положенный на горку, замирает?


Тот, кто внимательно наблюдал за установкой, сразу догадается, что даже если каток едет вверх по горке, он в действительности опускается. Ведь в отличие от цилиндров или санок, съезжающих с горы, у катка расстояние до опоры меняется. Так, по мере продвижения катка в горку просвет между рейками ширится и каток на них опирается всё более узкими частями, катится по меньшему радиусу, приближая ось к рейкам. В зависимости от того, что меняется быстрее – высота реек или соответствующее ей снижение катка, зависит, поедет ли он вверх или вниз. Каток всегда стремится опуститься – занять состояние с наименьшей потенциальной энергией, как сказал бы физик. Если же высота центра тяжести не меняется, – поднятие по рейке компенсируется таким же опусканием катка, – он стоит, как на ровном.
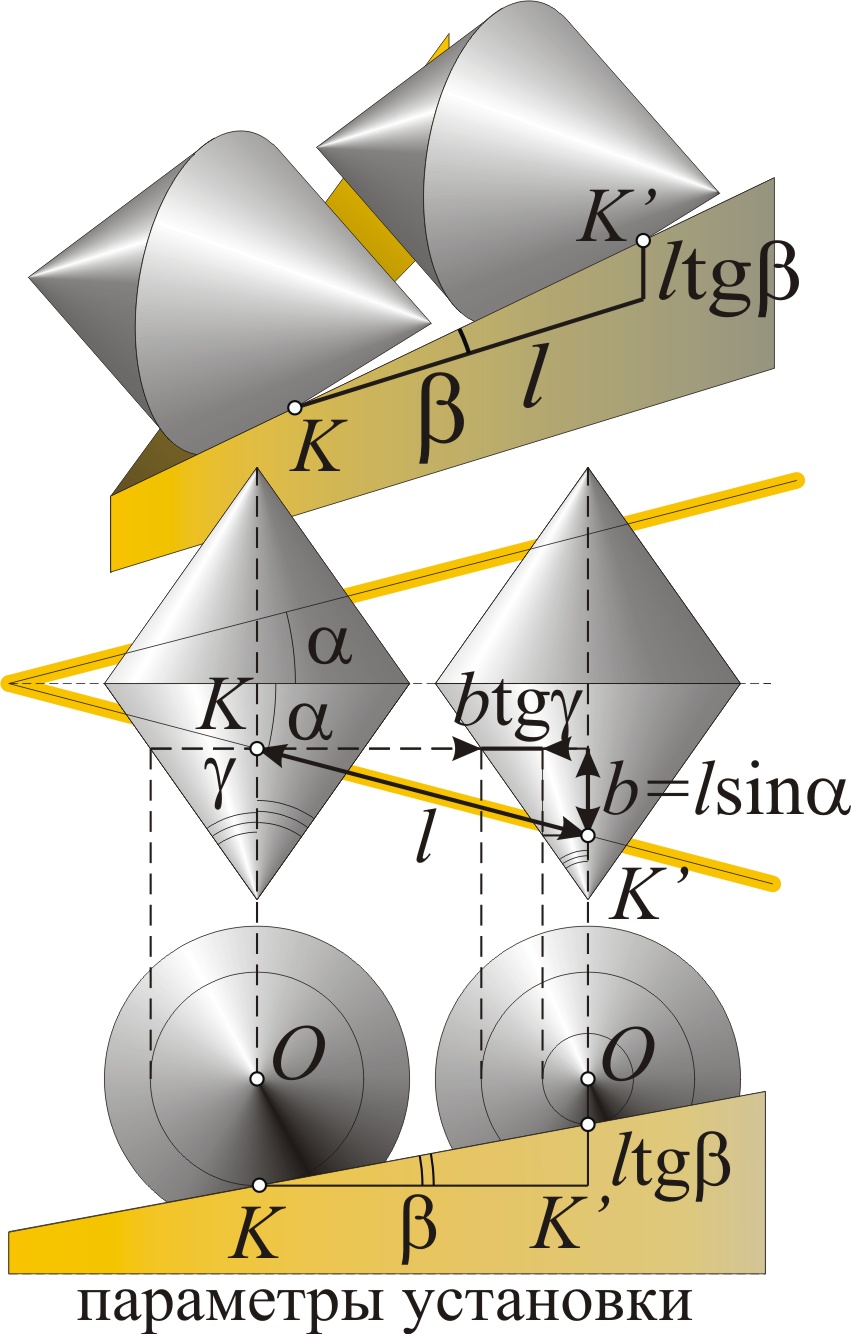
Отсюда легко найти то самое критическое соотношение параметров установки. Очевидно, таких параметров, способных влиять на исход опыта, только три – угол 2α между рейками, угол β их скоса и угол γ конусности катка, составляемый образующей конуса с его осью. Если каток пройдёт вдоль рейки расстояние l, точка его опоры K поднимется на ltgβ. При этом точки опоры катка разойдутся от его средней плоскости (от общего основания конусов) на расстояния b=lsinα. А радиус качения уменьшится на btgγ= lsinαtgγ. Итак, поднятие опоры катка на ltgβ от въезда в горку сопровождается его опусканием на lsinαtgγ от сближения оси O с рейкой. Если первое больше второго, – каток съезжает, а если меньше – катится в гору. Если же эти изменения высоты компенсируют друг друга: ltgβ= lsinαtgγ, то высота центра O катка не меняется. То есть, если выполнено критическое соотношение tgβ= sinαtgγ, каток не пойдёт ни вверх, ни вниз по горке – ему безразлично, куда ехать и где находиться.
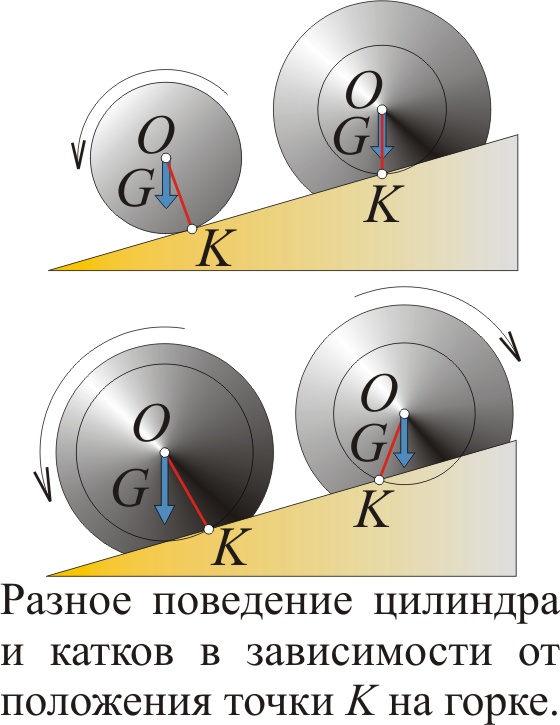
Однако энергетические соображения не слишком-то наглядны. Они позволяют узнать исход опыта, сказать, как поведёт себя каток, но не объясняют почему. Поэтому проще понять, почему каток движется так, а не иначе, рассматривая действующие на него силы. Ведь движение санок с горы вниз обычно объясняют не тем, что это им "выгодно", а тем, что их притягивает Земля. Цилиндр катится с горки не потому, что знает где "лучше", а поскольку действующая на него сила тяжести G создаёт вращательный момент относительно точки опоры K, заставляющий его кубарем слетать вниз. Для цилиндра, как легко понять, эта точка касания K всегда лежит по горке выше его центра тяжести O. Поэтому момент направлен так, что катит цилиндр вниз. У катка же точка K может находиться ближе к началу горки или под центром тяжести O. Соответственно момент направлен так, что каток поедет вверх или останется недвижим. Это напоминает известный опыт с катушкой, которая в зависимости от угла, под которым тянут намотанную на неё нить, катится к нам или от нас.
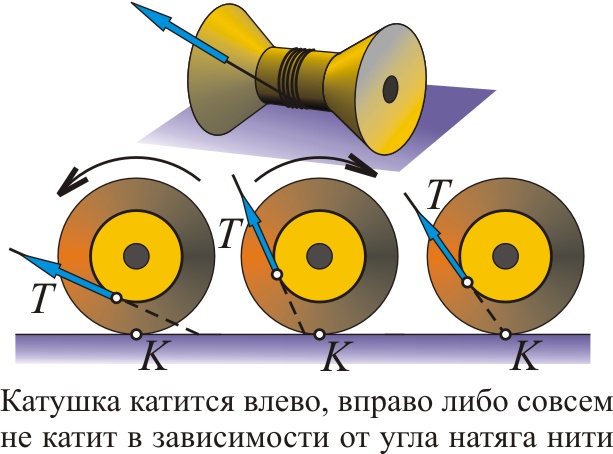
Итак, чтобы найти критическое соотношение параметров, надо рассмотреть касание линии рейки одного из конусов катка. Как сказано, дабы каток находился в покое, точка касания K должна лежать точно под осью O конуса. То есть перпендикуляр KO к оси конуса должен быть вертикален. Значит угол, образованный рейкой-касательной и KO, равен 90–β. Отсюда из геометрии конуса легко придём к тому же соотношению tgβ= sinαtgγ, при котором каток остаётся неподвижен. Меняя один из углов, мы смещаем точку K. Соответственно для биконуса горка оказывается "горизонтальной" либо наклонной "вправо" или "влево".
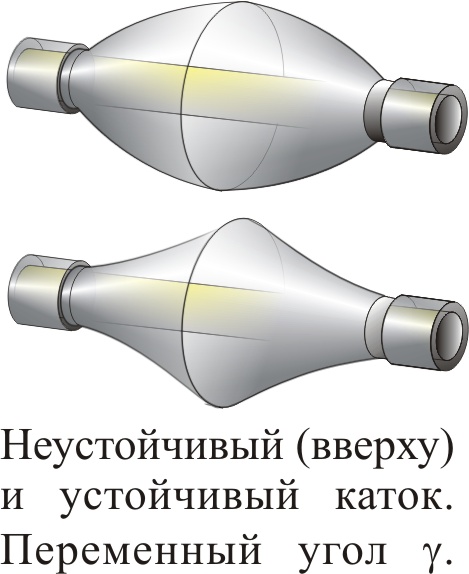
Теперь, когда ясен смысл критического соотношения, его можно не только проверить на практике, измерив транспортиром все углы, но и применить для видоизменения опыта. Так, становится ясно, что не обязательно использовать каток, имеющий вид биконуса типа "поплавок", конусы можно соединять не только основаниями, но и вершинами – биконус типа "катушка". Кстати, простая катушка для ниток и впрямь может послужить таким катком. Собирая такой каток из конических верхушек бутылок, их надо соединять уже не основаниями, а горлышками, которые проще всего скрепить, свинтив горловины общей крышкой со срезанным дном. Это будет соответствовать изменению угла γ на -γ. Значит, по формуле надо сменить и знак угла β, – чтобы рейки соединялись уже не узкими, а широкими концами.

Иллюзию поднятия катка вверх по горке можно усилить, если сделать угол β большим (градусов в 45). Понятно, что одновременно надо увеличить углы α и γ, так что в итоге каток станет больше похож на две сложенных вместе тарелки. Или можно попробовать сделать опускание центра тяжести малозаметным. Для чего надо предельно уменьшить угол α, чтобы рейки выглядели почти параллельными. Угол γ при этом нужно, напротив, сделать большим. А чтобы размер катка был не слишком велик, а его конусность не бросалась в глаза, надо оставить только его концевые части, катящиеся по рейкам, как колёса вагонов по рельсам. Поэтому конусные колёса должны соединяться не основаниями или вершинами, а общей осью.
Если теперь присоединить проволокой к коробку пару таких колёсных осей (а проще –пару простых катушек), получится настоящая тележка-самокатка, способная ехать в гору, с которой другие предметы (цилиндры и бруски) съезжают. Такая тележка кажется чудом, –столь сложно у неё заметить снижение центра масс при въезде в горку. Если же соединить колёса с тележкой жёстко и смазать "рельсы", можно получить и сани, "въезжающие в гору".

Теперь можно рассмотреть и более сложные формы. Что будет, если мы изогнём картонные рейки? Это приведёт к переменности угла α вдоль горки. Если угол α нарастает, то каток будет выше некоторой критической точки закатываться вверх, а ниже её – спускаться вниз, то есть будет всегда удаляться от этой точки. Если же картонные рейки постепенно сходятся, и угол α уменьшается, каток будет всегда стремиться к точке с критическим углом α. Доехав до неё, он станет, как в яме, кататься туда-сюда, пока не замрёт в этой точке. Другой вариант – это когда рейки плоские (угол α постоянен), зато меняется β, – гора меняет наклон. На ней тоже будет критическая точка при некотором угле β, являющаяся точкой устойчивого или неустойчивого равновесия катка, смотря по тому, вогнута горка или выпукла.


Наконец третий вариант: когда α и β постоянны, но меняется угол γ. Такое возможно, если мы используем каток не из конусов, а из других тел вращения, имеющих криволинейную образующую. Такой каток можно сделать из двух пластиковых бутылок, но не с конусной, а с закруглённой верхушкой. Также можно использовать, вместо конических, скруглённые наконечники от ручек или же шарики для пинг-понга. Для каждого из таких катков есть своё определённоё критическое место на горке, в точке контакта с которым угол γ равен критическому. Положенный выше этого места каток катится вверх, а ниже – вниз. Для того чтобы эта точка служила местом устойчивого равновесия, необходимо применить катки с вогнутой поверхностью. Наконец возможны сложные комбинации всех трёх вариантов.
Но может ли всё это иметь практическое применение? Нельзя ли, к примеру, построить железную дорогу, идущую "под гору" в обе стороны, чтобы поезд сам по себе, без затрат энергии мог доехать туда и обратно? Казалось бы, достаточно уложить рельсы наподобие наклонных расходящихся реек, и сделать поезду два комплекта колёс – одни с углом γ большим критического, другие – с меньшим. Доехал поезд до конечной станции, сменили ему колёса, и он сам пойдёт назад. А как доедет, ему снова сменят колёса, и он тронется в обратный путь. Или же сконструировать поезд с изменяемой геометрией колеса. Конечно, такой поезд, сам идущий в оба конца, невозможен, как и любой вечный двигатель. Это ясно из энергетических соображений. Раз центр масс всегда спускается, то дабы поезд сам шёл туда и обратно, на конечных станциях придётся либо поднимать его с затратами энергии, либо уменьшать размеры колёс, пока они не станут нулевыми. Так что, каких чудо-паровозов и едущих в гору тележек ни выдумывай, а всё равно найдётся … здесь какой-нибудь обман.
С.Семиков
Дата установки: 04.12.2008
[вернуться к содержанию сайта]
